练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．为了解参加某种知识竞赛的10 000名学生的成绩，从中抽取一个容量为500的样本，那么采用什么抽样方法比较恰当？写出抽样过程．

    分析 因需要研究的个体很多，且差异不明显，适宜用系统抽样；
    抽样过程是：（1）编号，（2）确定组数与组距，
    （3）在第一组中用简单随机抽样抽取1个号码，
    （4）以此为起始号码，间隔相等抽取所有的号码，组成样本．

    解答 解：适宜选用系统抽样，抽样过程如下：
    （1）随机地将这10 000名学生编号为1，2，3，…，10 000；
    （2）将总体按编号顺序均分成500个部分，每部分包括20个个体；
    （3）在第一部分的个体编号1，2，3，…，20中，利用简单随机抽样抽取一个号码，比如是18；
    （4）以18为起始号码，每间隔20抽取一个号码，这样得到一个容量为500的样本：
    18，38，58，…，9 978，9 998．

    点评 本题考查了系统抽样方法的应用问题，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．下面是关于公差d＞0的等差数列{an}的四个命题：p1：数列{an}是递增数列；p2：数列{an}的前n项和Sn是递增数列；p3：数列{$\frac{{a}_{n}}{n}$}是递增数列；p4：数列{an+nd}是递增数列．其中的真命题为（　　）
    A．p1，p2B．p3，p4C．p2，p3D．p1，p4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知正方形ABCD的边长是a，依次连接正方形ABCD的各边中点得到一个新的正方形，再依次连接新正方形的各边中点又得到一个新的正方形，按此规律，依次得到一系列的正方形，如图所示，现有一只小虫从A点出发，沿正方形的边逆时针方向爬行，每遇到新正方形的顶点时，沿这个新正方形的边逆时针方向爬行，如此下去，爬行了10条线段，则这10条线段的长度的和是（　　）
    A．$\frac{31}{128}（2+\sqrt{2}）a$B．$\frac{31}{64}（2+\sqrt{2}）a$C．$（1+\frac{{\sqrt{2}}}{32}）a$D．$（1-\frac{{\sqrt{2}}}{32}）a$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．设集合A={2}，B={x|ax-1=0，a∈R}，若A∩B=B，则a=0或$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．（Ⅰ）求证：$kC_n^k=nC_{n-1}^{k-1}$；
    （Ⅱ）在数学上，常用符号来表示算式，如记$\sum_{i=0}^n{a_i}={a_0}+{a_1}+{a_2}+…+{a_n}$，其中i∈N，n∈N*．
    ①若a0，a1，a2，…，an成等差数列，且a0=0，求证：$\sum_{i=0}^n{（{a_i}•C_n^i}）={a_n}•{2^{n-1}}$；
    ②若$\sum_{k=1}^{2n}{{{（1+x）}^k}}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_{2n}}{x^{2n}}$，${b_n}=\sum_{i=0}^n{{a_{2i}}}$，记${d_n}=1+\sum_{i=1}^n{[{{（-1）}^i}}•{b_i}•C_n^i]$，且不等式t•（dn-1）≤bn恒成立，求实数t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

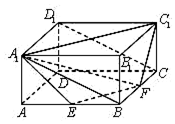    7．如图，在长方体ABCD-A1B1C1D1中，AA1=1，AB=AD=2，E，F分别是棱AB，BC的中点，证明A1，C1，F，E四点共面，并求点B到平面A1EF的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．如图，梯形ABCD中，|$\overrightarrow{AD}$|=|$\overrightarrow{BC}$|，$\overrightarrow{EF}$∥$\overrightarrow{AB}$∥$\overrightarrow{CD}$，则相等向量是（　　）
    A．$\overrightarrow{AD}$与$\overrightarrow{BC}$B．$\overrightarrow{OA}$与$\overrightarrow{OB}$C．$\overrightarrow{AC}$与$\overrightarrow{BD}$D．$\overrightarrow{EO}$与$\overrightarrow{OF}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知函数f（x）=$\frac{lnx}{x}$-1．
    （I）求函数f（x）的单调区间；
    （II）设m＞0，若函数g（x）=2xf（x）-x2+2x+m在$[{\frac{1}{e}，e}]$上有两个零点，求实数m的取值范围．
    （III）证明：对?n∈N*，不等式$ln{（\frac{1+n}{n}）^e}＜\frac{1+n}{n}$成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．如图在直角梯形ABCP中，AP∥BC，AB=BC=$\frac{1}{2}$AP=2，D是AP的中点，E，G分别为PC，CB的中点，将△PCD沿CD折起，使得PD⊥平面ABCD，F为线段PD上一动点．当二面角G-EF-D的大小为$\frac{π}{4}$时，求FG与平面PBC所成角的余弦值．

    查看答案和解析>>

    同步练习册答案