Question

4．一个正方体的平面展开图及该正方体的直观图的示意图如图所示．

（Ⅰ）请按字母F，G，H标记在正方体相应地顶点处（不需要说明理由）
（Ⅱ）判断平面BEG与平面ACH的位置关系．并说明你的结论．
（Ⅲ）证明：直线DF⊥平面BEG．

Answer 1

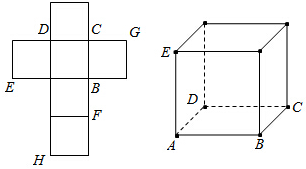
分析 （Ⅰ）直接标出点F，G，H的位置．
（Ⅱ）先证BCHE为平行四边形，可知BE∥平面ACH，同理可证BG∥平面ACH，即可证明平面BEG∥平面ACH．
（Ⅲ）连接FH，由DH⊥EG，又DH⊥EG，EG⊥FH，可证EG⊥平面BFHD，从而可证DF⊥EG，同理DF⊥BG，即可证明DF⊥平面BEG．

解答 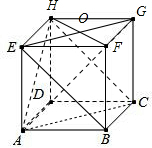解：（Ⅰ）点F，G，H的位置如图所示．
（Ⅱ）平面BEG∥平面ACH，证明如下：
∵ABCD-EFGH为正方体，
∴BC∥FG，BC=EH，
又FG∥EH，FG=EH，
∴BC∥EH，BC=EH，
∴BCHE为平行四边形．
∴BE∥CH，
又CH?平面ACH，BE?平面ACH，
∴BE∥平面ACH，
同理BG∥平面ACH，
又BE∩BG=B，
∴平面BEG∥平面ACH．
（Ⅲ）连接FH，
∵ABCD-EFGH为正方体，
∴DH⊥EG，
又∵EG?平面EFGH，
∴DH⊥EG，
又EG⊥FH，EG∩FH=O，
∴EG⊥平面BFHD，
又DF?平面BFHD，
∴DF⊥EG，
同理DF⊥BG，
又∵EG∩BG=G，
∴DF⊥平面BEG．

点评 本题主要考查了简单空间图形的直观图、空间线面平行与垂直的判定与性质等基础知识，考查了空间想象能力和推理论证能力，属于中档题．