
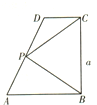
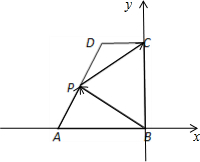
 如图所示,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设
如图所示,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设| AP |
| AD |
| PB |
| PC |
| 2 |
| AP |
| AD |
| BP |
| BA |
| AP |
| PC |
| PB |
| BC |
| PB |
| PC |
| 4 |
| 5 |
| 4 |
| 5 |
| 4+a2 |
| 2(a2+1) |
| 2 |
| 2 |
| 2 |
| AP |
| AD |
| BP |
| BA |
| AP |
| PC |
| PB |
| BC |
| PB |
| PC |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4+a2 |
| 2(a2+1) |
| 2 |
| 2 |
| 2 |


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
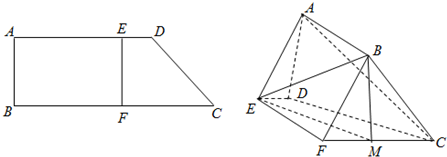
 如图,已知四边形ABCD是正方形,PD⊥平面ABCD,CD=PD=2EA,PD∥EA,F,G,H分别为PB,BE,PC的中点.
如图,已知四边形ABCD是正方形,PD⊥平面ABCD,CD=PD=2EA,PD∥EA,F,G,H分别为PB,BE,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
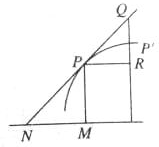 微积分的创立与求曲线的切线是密不可分的,历史上有很多关于曲线的研究.如图,设PN是曲线的切线,下面是两位数学家的说法:
微积分的创立与求曲线的切线是密不可分的,历史上有很多关于曲线的研究.如图,设PN是曲线的切线,下面是两位数学家的说法:| PM |
| NM |
| P′R |
| PR |
| dy |
| dx |
| A、Barrow正确,Leibniz错误 |
| B、Leibniz正确,Barrow错误 |
| C、Barrow,Leibniz都正确 |
| D、Barrow,Leibniz都错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:
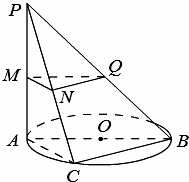 如图,⊙O在平面α内,AB是⊙O的直径,PA⊥平面α,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.
如图,⊙O在平面α内,AB是⊙O的直径,PA⊥平面α,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com