
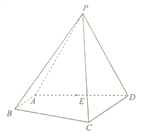
【题目】如图,在四棱锥![]() 中,
中, ![]() 是等边三角形,
是等边三角形, ![]() 为
为![]() 的中点,四边形
的中点,四边形![]() 为直角梯形,
为直角梯形, ![]()
![]()
![]()
![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的体积;
的体积;
(3)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?说明理由.
?说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)存在
;(3)存在![]() 为
为![]() 中点.
中点.
【解析】试题分析:(1)由![]()
![]() 根据线面垂直的判定定理可证明
根据线面垂直的判定定理可证明![]() 平面
平面![]() ,再利用面面垂直的判定定理可得结论;(2)连接
,再利用面面垂直的判定定理可得结论;(2)连接![]() 因为△
因为△![]() 为等边三角形,
为等边三角形, ![]() 为
为![]() 中点,所以
中点,所以![]() .因为
.因为![]() 平面
平面![]() ,所以
,所以![]() ,由线面垂直的性质可得
,由线面垂直的性质可得![]() 平面
平面![]() ,即
,即![]() 是棱锥
是棱锥![]() 高,算出底面面积,利用棱锥的体积公式可得结果;(3)棱
高,算出底面面积,利用棱锥的体积公式可得结果;(3)棱![]() 上存在点
上存在点![]() ,使得
,使得![]() ∥平面
∥平面![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() 由中位线定理及线面平行的判定定理可得
由中位线定理及线面平行的判定定理可得![]() ∥平面
∥平面![]() ,可得平面
,可得平面![]() ∥平面
∥平面![]() .再利用面面平行的性质可得结论.
.再利用面面平行的性质可得结论.
试题解析:(1) 因为![]() ,
, ![]() ,
, ![]() ,
,
所以![]() 平面
平面![]() .因为
.因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)连接![]() .
.
因为△![]() 为等边三角形,
为等边三角形, ![]() 为
为![]() 中点,所以
中点,所以![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]()
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
所以![]() .
.
在等边△![]() 中,
中,![]() ,
,
![]() ,
,
所以![]() .
.
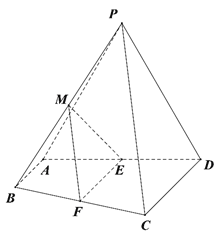
(3)棱![]() 上存在点
上存在点![]() ,使得
,使得![]() ∥平面
∥平面![]() ,此时点
,此时点![]() 为
为![]() 中点.取
中点.取![]() 中点
中点![]() ,连接
,连接![]() .因为
.因为![]() 为
为![]() 中点, 所以
中点, 所以![]() ∥
∥![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]() .因为
.因为![]() 为
为![]() 中点,
中点,
所以![]() ∥
∥![]() .因为
.因为![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]() .
.
因为![]() ,所以平面
,所以平面![]() ∥平面
∥平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]() .
.


科目:高中数学 来源: 题型:
【题目】在某批次的某种灯泡中,随机地抽取![]() 个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于![]() 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于![]() 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.
寿命(天) | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(Ⅰ)根据频率分布表中的数据,写出![]() ,
, ![]() 的值.
的值.
(Ⅱ)某人从灯泡样品中随机地购买了![]() 个,求
个,求![]() 个灯泡中恰有一个是优等品的概率.
个灯泡中恰有一个是优等品的概率.
(Ⅲ)某人从这个批次的灯泡中随机地购买了![]() 个进行使用,若以上述频率作为概率,用
个进行使用,若以上述频率作为概率,用![]() 表示此人所购买的灯泡中次品的个数,求
表示此人所购买的灯泡中次品的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
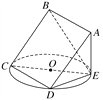
【题目】(2017·安徽名校阶段性测试)如图所示,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C,D的点,AE=3,圆O的直径CE=9.
(1)求证:平面ABE⊥平面ADE;
(2)求五面体ABCDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,![]() 为正三角形,且侧面PAB⊥底面ABCD,
为正三角形,且侧面PAB⊥底面ABCD, ![]() 为线段
为线段![]() 的中点,
的中点, ![]() 在线段
在线段![]() 上.
上.
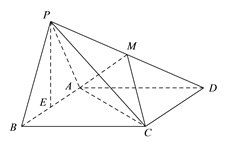
(I)当![]() 是线段
是线段![]() 的中点时,求证:PB // 平面ACM;
的中点时,求证:PB // 平面ACM;
(II)求证: ![]() ;
;
(III)是否存在点![]() ,使二面角
,使二面角![]() 的大小为60°,若存在,求出
的大小为60°,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com