Question

5．如图，ABCD-A₁B₁C₁D₁为正方体，下面结论错误的是（　　）

• A． BD∥平面CB₁D₁
• B． AC₁⊥B₁C
• C． AC₁⊥平面CB₁D₁
• D． 直线CC₁与平面CB₁D₁所成的角为45°

Answer 1

分析 利用正方体的性质，利用线线平行的判定，线面平行、垂直的判定和性质，逐一分析研究各个选项的正确性．

解答 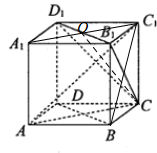解：由正方体的性质得BD∥B₁D₁，所以BD∥平面CB₁D₁，故①正确；
由正方体的性质得B₁C⊥AB、B₁C⊥BC₁，∴BC₁⊥平面ABC₁，∴AC₁⊥B₁C，故②正确；
由②知AC₁⊥B₁C，同理可证AC₁⊥B₁D₁，∴AC₁⊥平面CB₁D₁ ，故③正确．
连结A₁C₁交B₁D₁于O，则∠C₁CO即为直线CC₁与平面CB₁D₁所成的角，
显然此角小于∠C₁CB₁=45°，故④不正确．
故选：D．
（注：本题通过建立空间直角坐标系亦可解决）

点评 本题考查线面平行的判定，利用三垂线定理证明2条直线垂直，线面垂直的判定，求异面直线成的角，注意解题方法的积累，属于中档题．