
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为2,线段D1B1上有两个动点E、F,且EF=1,则下列结论中错误的是( ) 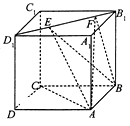
A.AC⊥BE
B.AA1∥平面BEF
C.三棱锥A﹣BEF的体积为定值
D.△AEF的面积和△BEF的面积相等
【答案】D
【解析】解:如图所示, 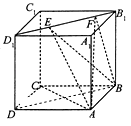
对于A,AC⊥平面BB1D1D,又BE平面BB1D1D,
∴AC⊥BE,故A正确;
对于B,∵AA1∥平面BDD1B1 , 又E、F在直线D1B1上运动,
∴平面BEF与平面BDD1B1重合,
∴AA1∥平面BEF,故B正确;
对于C,由于点B到直线B1D1的距离不变,故△BEF的面积为定值;
又点A到平面BEF的距离为 ![]() =
= ![]() ,故V三棱锥A﹣BEF为定值,C正确;
,故V三棱锥A﹣BEF为定值,C正确;
对于D,∵点A、B到直线B1D1的距离不相等,
∴△AEF的面积与△BEF的面积不相等,故D错误.
故选:D.
选项A中,由AC⊥平面BB1D1D得出AC⊥BE,正确;
选项B中,由AA1∥平面BDD1B1 , 平面BEF与平面BDD1B1重合,得出AA1∥平面BEF,正确;
选项C中,由△BEF的面积为定值,点A到平面BEF的距离定值,得V三棱锥A﹣BEF为定值,正确;
选项D中,由点A、B到直线B1D1的距离不相等,得△AEF的面积与△BEF的面积不相等,D错误.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x+2 ![]() sin2x+1﹣
sin2x+1﹣ ![]() .
.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)当x∈[ ![]() ,
, ![]() ]时,求函数f(x)的值域.
]时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为a的正方体ABCD﹣A1B1C1D1中,E、F分别是AB、BC的中点,EF与BD交于点G,M为棱BB1上一点. 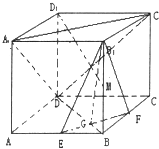
(1)证明:EF∥平面 A1C1D;
(2)当B1M:MB的值为多少时,D1M⊥平面 EFB1 , 证明之;
(3)求点D到平面 EFB1的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆(x+2)2+y2=5关于直线x﹣y+1=0对称的圆的方程为( )
A.(x﹣2)2+y2=5
B.x2+(y﹣2)2=5
C.(x﹣1)2+(y﹣1)2=5
D.(x+1)2+(y+1)2=5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生对“两个一百年”奋斗目标、实现中华民族伟大复兴中国梦的“关注度”(单位:天),某中学团委在全校采用随机抽样的方法抽取了80名学生(其中男女人数各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组学生的月“关注度”分为6组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
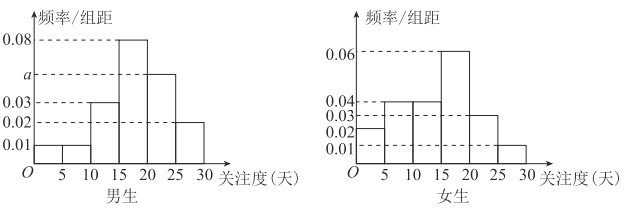
(1)求![]() 的值;
的值;
(2)求抽取的80名学生中月“关注度”不少于15天的人数;
(3)在抽取的80名学生中,从月“关注度”不少于25天的人中随机抽取2人,求至少抽取到1名女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x+1)是定义在R上的周期为2的偶函数,当x∈[1,2)时,f(x)=log2x,设a=f( ![]() ),
), ![]() ,c=f(1),则a,b,c的大小关系为( )
,c=f(1),则a,b,c的大小关系为( )
A.a<c<b
B.c<a<b
C.b<c<a
D.c<b<a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn满足Sn=a(Sn﹣an+1)(a为常数,且a>0),且a3是6a1与a2的等差中项.
(1)求{an}的通项公式;
(2)设bn=anlog2an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f(x)的定义域为R,并且满足f(x+y)=f(x)+f(y), ![]() ,且当x>0时,f(x)>0.
,且当x>0时,f(x)>0.
(1)求f(0)的值;
(2)判断函数的奇偶性;
(3)如果f(x)+f(2+x)<2,求x取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com