
分析 (1)求出函数的导数,令x=1,x=-1,得到方程,解得a=1,求得切线的斜率和切点,由点斜式方程可得切线方程;
(2)存在x∈(1,+∞)使得函数f(x)<m成立,即有m>f(x)min,求出函数f(x)在(1,+∞)的单调区间,求得最小值即可.
解答 解:(1)函数f(x)=ax3+x2f′(1)+1的导数
f′(x)=3ax2+2xf′(1),
令x=1,则f′(1)=3a+2f′(1),即为f′(1)=-3a,
由f′(-1)=9,可得3a-2•(-3a)=9,
解得a=1,即有f′(1)=-3,
则f(x)=x3-3x2+1,
即有f(1)=1-3+1=-1,
则f(x)在x=1处的切线方程为y+1=-3(x-1),
即有3x+y-2=0;
(2)f(x)=x3-3x2+1的导数f′(x)=3x2-6x,
当1<x<2时,f′(x)<0,f(x)递减;
当x>2时,f′(x)>0,f(x)递增.
即有x=2处,f(x)取得极小值,且为最小值,且f(2)=-3,
存在x∈(1,+∞)使得函数f(x)<m成立,
即有m>f(x)min=-3,
故m的取值范围为(-3,+∞).
点评 本题考查导数的运用:求切线方程和单调区间、极值和最值,同时考查不等式存在性问题,注意转化为求函数的最值问题,属于中档题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:填空题
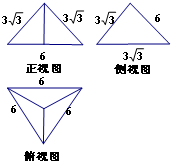 正四面体(即各条棱长均相等的三棱锥)的棱长为6,某学生画出该正四面体的三视图如下,其中有一个视图是错误的,则该视图修改正确后对应图形的面积为6$\sqrt{6}$.该正四面体的体积为18$\sqrt{2}$.
正四面体(即各条棱长均相等的三棱锥)的棱长为6,某学生画出该正四面体的三视图如下,其中有一个视图是错误的,则该视图修改正确后对应图形的面积为6$\sqrt{6}$.该正四面体的体积为18$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$i | C. | $\frac{4}{5}$i | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | [2,e) | C. | $({e+\frac{1}{e},+∞})$ | D. | $[{2,e+\frac{1}{e}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com