
【题目】设定义域为R的函数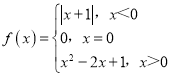 .
.
(1)在平面直角坐标系中作出函数f(x)的图象,并指出f(x)的单调区间(不需证明);
(2)若方程f(x)+5a=0有两个解,求出a的取值范围(不需严格证明,简单说明即可);
(3)设定义域为R的函数g(x)为偶函数,且当x≥0时,g(x)=f(x),求g(x)的解析式.
【答案】(1)函数f(x)的增区间为(﹣1,0),(1,+∞);减区间为(﹣∞,﹣1),(0,1),图象见解析
(2)![]()
(3)
【解析】
(1)作出函数f(x)的图象,由图象即可观察得出;
(2)方程f(x)+5a=0有两个解,等价于函数f(x)的图象与直线![]() 有两个交点,由图即可求出;
有两个交点,由图即可求出;
(3)先求出x≥0时,g(x)的解析式,再根据偶函数的性质,求出x<0时,g(x)
的解析式,即可求出定义在![]() 上的g(x)的解析式.
上的g(x)的解析式.
(1)作出函数f(x)的图象,如图所示:
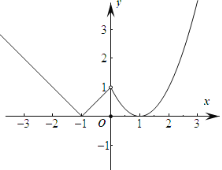
函数f(x)的增区间为(﹣1,0),(1,+∞),减区间为(﹣∞,﹣1),(0,1).
(2)要使方程f(x)+5a=0有两个解,等价于函数f(x)的图象与直线![]() 有两个交点,由图可知,﹣5a≥1,解得
有两个交点,由图可知,﹣5a≥1,解得![]() .故实数a的取值范围为
.故实数a的取值范围为![]() ;
;
(3)由题意,当x=0时,g(x)=0,当x>0时,g(x)=x2﹣2x+1,
设x<0,则﹣x>0,故g(﹣x)=(﹣x)2﹣2(﹣x)+1=x2+2x+1,
又函数g(x)为偶函数,故g(x)=g(﹣x)=x2+2x+1(x<0),
综上,函数g(x)的解析式为 .
.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,离心率为
,离心率为![]() ,圆
,圆![]() ,
,![]() 是椭圆的左右顶点,
是椭圆的左右顶点,![]() 是圆
是圆![]() 的任意一条直径,
的任意一条直径,![]() 面积的最大值为2.
面积的最大值为2.
(1)求椭圆![]() 及圆
及圆![]() 的方程;
的方程;
(2)若![]() 为圆
为圆![]() 的任意一条切线,
的任意一条切线,![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,求
,求![]() 的取直范围.
的取直范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(l)求曲线![]() 和直线
和直线![]() 的极坐标方程;
的极坐标方程;
(2)已知直线![]() 分别与曲线
分别与曲线![]() 、曲线
、曲线![]() 交异于极点的
交异于极点的![]() ,若
,若![]() 的极径分别为
的极径分别为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PD⊥底面ABCD,底面ABCD是边长为a的正方形,且PD=a.
(1)求四棱锥P﹣ABCD的体积;
(2)若E为PC中点,求证:PA∥平面BDE;
(3)求直线PB与平面ABCD所成角的正切值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市政府为了节约生活用电,计划在本市试行居民生活用电定额管理,即确定一户居民月用电量标准a,用电量不超过a的部分按平价收费,超出a的部分按议价收费![]() 为此,政府调查了100户居民的月平均用电量
为此,政府调查了100户居民的月平均用电量![]() 单位:度
单位:度![]() ,以
,以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图所示.
分组的频率分布直方图如图所示.
![]() 根据频率分布直方图的数据,求直方图中x的值并估计该市每户居民月平均用电量
根据频率分布直方图的数据,求直方图中x的值并估计该市每户居民月平均用电量![]() 的值;
的值;
![]() 用频率估计概率,利用
用频率估计概率,利用![]() 的结果,假设该市每户居民月平均用电量X服从正态分布
的结果,假设该市每户居民月平均用电量X服从正态分布![]()
![]() 估计该市居民月平均用电量介于
估计该市居民月平均用电量介于![]() 度之间的概率;
度之间的概率;
![]() 利用
利用![]() 的结论,从该市所有居民中随机抽取3户,记月平均用电量介于
的结论,从该市所有居民中随机抽取3户,记月平均用电量介于![]() 度之间的户数为
度之间的户数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房产中介公司2017年9月1日正式开业,现对其每个月的二手房成交量进行统计,![]() 表示开业第
表示开业第![]() 个月的二手房成交量,得到统计表格如下:
个月的二手房成交量,得到统计表格如下:

(1)统计中常用相关系数![]() 来衡量两个变量之间线性关系的强弱.统计学认为,对于变量
来衡量两个变量之间线性关系的强弱.统计学认为,对于变量![]() ,如果
,如果![]() ,那么相关性很强;如果
,那么相关性很强;如果![]() ,那么相关性一般;如果
,那么相关性一般;如果![]() ,那么相关性较弱.通过散点图初步分析可用线性回归模型拟合
,那么相关性较弱.通过散点图初步分析可用线性回归模型拟合![]() 与
与![]() 的关系.计算
的关系.计算![]() 的相关系数
的相关系数![]() ,并回答是否可以认为两个变量具有很强的线性相关关系(计算结果精确到0.01)
,并回答是否可以认为两个变量具有很强的线性相关关系(计算结果精确到0.01)
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (计算结果精确到0.01),并预测该房产中介公司2018年6月份的二手房成交量(计算结果四舍五入取整数).
(计算结果精确到0.01),并预测该房产中介公司2018年6月份的二手房成交量(计算结果四舍五入取整数).
(3)该房产中介为增加业绩,决定针对二手房成交客户开展抽奖活动.若抽中“一等奖”获6千元奖金;抽中“二等奖”获3千元奖金;抽中“祝您平安”,则没有奖金.已知一次抽奖活动中获得“一等奖”的概率为![]() ,获得“二等奖”的概率为
,获得“二等奖”的概率为![]() ,现有甲、乙两个客户参与抽奖活动,假设他们是否中奖相互独立,求此二人所获奖金总额
,现有甲、乙两个客户参与抽奖活动,假设他们是否中奖相互独立,求此二人所获奖金总额![]() (千元)的分布列及数学期望.
(千元)的分布列及数学期望.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某长产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量 | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若近几年该农产品每千克的价格![]() (单位:元)与年产量
(单位:元)与年产量![]() 满足的函数关系式为
满足的函数关系式为![]() ,且每年该农产品都能售完.
,且每年该农产品都能售完.
①根据(1)中所建立的回归方程预测该地区2018(![]() )年该农产品的产量;
)年该农产品的产量;
②当![]() (
(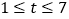 )为何值时,销售额
)为何值时,销售额![]() 最大?
最大?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: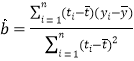 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从集合![]() 的所有非空子集中,等可能地取出
的所有非空子集中,等可能地取出![]() 个.
个.
(1)若![]() ,求所取子集的元素既有奇数又有偶数的概率;
,求所取子集的元素既有奇数又有偶数的概率;
(2)若![]() ,记所取子集的元素个数之差为
,记所取子集的元素个数之差为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com