
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
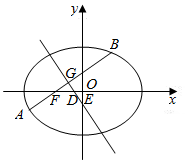 椭圆C:$\frac{x^2}{4}$+$\frac{y^2}{3}$=1的左焦点为F,右顶点为A1,过点F斜率为k的直线交椭圆C于A,B两点,线段AB的中点为G,线段AB的垂直平分线交x轴于点D,交y轴于点E,O是坐标原点,记△GFD的面积为S1,记△OED的面积为S2
椭圆C:$\frac{x^2}{4}$+$\frac{y^2}{3}$=1的左焦点为F,右顶点为A1,过点F斜率为k的直线交椭圆C于A,B两点,线段AB的中点为G,线段AB的垂直平分线交x轴于点D,交y轴于点E,O是坐标原点,记△GFD的面积为S1,记△OED的面积为S2查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 定义运算a*b为执行如图所示的程序框图输出的S值,则(sin$\frac{5π}{12}}$)*(${cos\frac{5π}{12}}$)的值为( )
定义运算a*b为执行如图所示的程序框图输出的S值,则(sin$\frac{5π}{12}}$)*(${cos\frac{5π}{12}}$)的值为( )| A. | $\frac{{2-\sqrt{3}}}{4}$ | B. | $\frac{{2+\sqrt{3}}}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
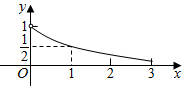 已知奇函数y=$\left\{\begin{array}{l}{{a}^{x},x>0}\\{f(x),x<0}\end{array}\right.$(a>0且a≠1)的部分图象如图所示,那么f(x)=( )
已知奇函数y=$\left\{\begin{array}{l}{{a}^{x},x>0}\\{f(x),x<0}\end{array}\right.$(a>0且a≠1)的部分图象如图所示,那么f(x)=( )| A. | 2x | B. | $-{(\frac{1}{2})^x}$ | C. | ${({\frac{1}{2}})^x}$ | D. | -2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
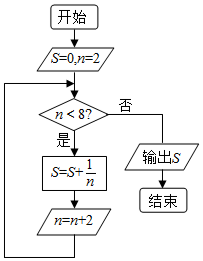 如图所示,执行程序框图,输出结果( )
如图所示,执行程序框图,输出结果( )| A. | $\frac{5}{12}$ | B. | $\frac{7}{12}$ | C. | $\frac{11}{12}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com