
| 45 |
| x |
| 75 |
| 5 |
| 5 |
| 45+30 |
| 1 |
| 15 |
| 45 |
| x |
| 75 |
| 5 |
| 12 |
| 20 |
| 3 |
| 5 |


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
 如图,四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
如图,四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
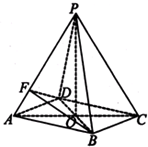 如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD=
如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD=| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
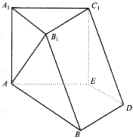 如图,在六面体A1B1C1D1中,平面A1B1C1∥平面ABDE,△A1B1C1是正三角形,四边形AA1B1B是直角梯形,AB⊥AA1,四边形AEC1A1为正方形,四边形ABDE是等腰梯形,AB∥DE,AB=2AE=2DE=2.
如图,在六面体A1B1C1D1中,平面A1B1C1∥平面ABDE,△A1B1C1是正三角形,四边形AA1B1B是直角梯形,AB⊥AA1,四边形AEC1A1为正方形,四边形ABDE是等腰梯形,AB∥DE,AB=2AE=2DE=2.查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 某校高三年段共有1000名学生,将其按专业发展取向分成普理、普文、艺体三类,如图是这三类的人数比例示意图.为开展某项调查,采用分层抽样的方法从这1000名学生中抽取一个容量为10的样本.
某校高三年段共有1000名学生,将其按专业发展取向分成普理、普文、艺体三类,如图是这三类的人数比例示意图.为开展某项调查,采用分层抽样的方法从这1000名学生中抽取一个容量为10的样本.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com