
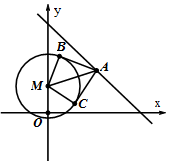
 ԲM��x2+y2-2y=24��ֱ��l��x+y=11��l��һ��A�ĺ�����Ϊa������A��ԲM����������l1��l2���е�ΪB��C��
ԲM��x2+y2-2y=24��ֱ��l��x+y=11��l��һ��A�ĺ�����Ϊa������A��ԲM����������l1��l2���е�ΪB��C������ ��1�����õ㵽ֱ�ߵľ��빫ʽ����ֱ�����б�ʣ�
��2����l1��l2ʱ���ı���MCABΪ�����Σ����a��ֵ����$��\overrightarrow{AB}��\overrightarrow{AC}��$=2�ȣ���$\overrightarrow{AB}$•$\overrightarrow{AC}$=|AB|2��1-2sin2�ȣ�����$\overrightarrow{AB}$•$\overrightarrow{AC}$=��AM2-25����1-$\frac{50}{A{M}^{2}}$��=AM2+$\frac{25��50}{2A{M}^{2}}$-75����Բ��M��ֱ��l�ľ�����$5\sqrt{2}$��AM2��50��$\overrightarrow{AB}$•$\overrightarrow{AC}$��50+$\frac{25��50}{50}$-75=0���ʵ�A�����ڣ�
��3��������Բ������������������ֱ�߷��̣��ҳ����㣮
��� �⣺��1��ԲM��x2+��y-1��2=25��Բ��M��0��1�����뾶r=5��A��0��11����
�����ߵķ���Ϊy=k x+11��Բ�ľ�d=$\frac{10}{\sqrt{{k}^{2}+1}}$=5��
��k=��$\sqrt{3}$������ֱ��l1��l2�ķ���Ϊy=��$\sqrt{3}$x+11
��2����l1��l2ʱ���ı���MCABΪ�����Σ�
��|AM|+$\sqrt{2}$|MB|=5$\sqrt{2}$
��A��a��11-a����M��0��1���� $\sqrt{{a}^{2}+��10-a��^{2}}$=$5\sqrt{2}$
a2-10a+25=0��a=5
��$��\overrightarrow{AB}��\overrightarrow{AC}��$=2�ȣ���
$\overrightarrow{AB}$•$\overrightarrow{AC}$=|AB|2��1-2sin2�ȣ���
��sin��=$\frac{r}{|AM|}$����$\overrightarrow{AB}$•$\overrightarrow{AC}$=��AM2-25����1-$\frac{50}{A{M}^{2}}$��=AM2+$\frac{25��50}{2A{M}^{2}}$-75��
��Բ��M��ֱ��l�ľ�����$5\sqrt{2}$
��AM2��50��$\overrightarrow{AB}$•$\overrightarrow{AC}$��50+$\frac{25��50}{50}$-75=0���ʵ�A�����ڣ�
��3����A��a��b������a+b=1 �٣�
��AMΪֱ����Բ��ԲM����B��C��AB��ACΪ���ߣ�
��AMΪֱ����Բ����Ϊ��x��x-a��+��y-1����y-b��=0 ��
ԲM��x2+y2-2y=24 �ۣ�
��ʽ�ڢ�����ù�����BC���̣�24+2y-ax-��b+1��y+b=0������ٻ���
y-$\frac{7}{2}$=-$\frac{a}{10-a}$��x-$\frac{5}{2}$������֪P0 ��$\frac{5}{2}$��$\frac{7}{2}$����
�����⣺
���ȣ��ڣ�III�����������ǣ�������P0 ��$\frac{5}{2}$��$\frac{7}{2}$����ֱ�߽�Բx2+y2-2y=24 ��B��C���㣬�ֱ���B��CΪ�е���ԲM������l1��l2 �ཻ��A�㣬��A��x+y=11�ϣ�
֤������A��a��b������AMΪֱ����Բ��ԲM����B��C����֤AB��ACΪ���ߣ�
��AMΪֱ����Բ����Ϊ��x��x-a��+��y-1����y-b��=0
ԲM��x2+y2-2y=24��
��ʽ����ù�����BC���̣�24+2y-ax-��b+1��y+b=0��
���ڹ�����BC����ֱ�߹�����P0 ��$\frac{5}{2}$��$\frac{7}{2}$��������ɵ�a+b=11����֤��
���� ������Ҫ������ֱ����Բ��ϵ���㵽ֱ�߾��빫ʽ��ֱ�߷��̣�Բ�ۺ��Լ�������֤�����⣬�����⣮


 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a32+a72��a42+a62 | B�� | a32+a72��a42+a62 | ||
| C�� | a32+a72=a42+a62 | D�� | a32+a72��a42+a62�Ĵ�С��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
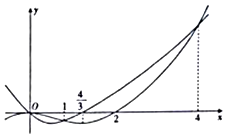
| A�� | ��0��4�� | B�� | $��{-�ޣ�1}������{\frac{4}{3}��4}��$ | C�� | $��{0��\frac{4}{3}}��$ | D�� | ��0��1������4��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a+$\frac{1}{a}$��2 | B�� | a+$\frac{1}{a}$��2 | C�� | a+$\frac{1}{a}$��-2 | D�� | |a+$\frac{1}{a}$|��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $\sqrt{5}$ | C�� | $\sqrt{3}$ | D�� | $\frac{\sqrt{5}}{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com