
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
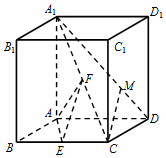 如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=$\frac{π}{3}$,E,F分别是BC,A1C的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=$\frac{π}{3}$,E,F分别是BC,A1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
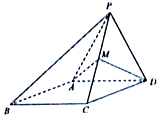 如图,四棱锥P-ABCD中,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是菱形,且∠ABC=60°,M为PC的中点.
如图,四棱锥P-ABCD中,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是菱形,且∠ABC=60°,M为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{n}>\frac{1}{m}$ | B. | |n|>|m| | C. | $\frac{n}{m}+\frac{m}{n}>2$ | D. | m+n>mn |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
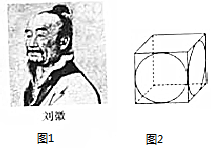 我国古代数学家刘徽(如图1)在学术研究中,不迷信古人,坚持实事求是,他对《九章算术》中“开立圆术”给出的公式产生质疑,为了证实自己的猜测,他引入了一种新的几何体“牟盒方盖”:一正方体相邻的两个侧面为底座两次内切圆柱切割,然后剔除外部,剩下的内核部分(如图2).如果“牟盒方盖”的主视图和左视图都是圆,则其俯视图形状为下列几幅图中的( )
我国古代数学家刘徽(如图1)在学术研究中,不迷信古人,坚持实事求是,他对《九章算术》中“开立圆术”给出的公式产生质疑,为了证实自己的猜测,他引入了一种新的几何体“牟盒方盖”:一正方体相邻的两个侧面为底座两次内切圆柱切割,然后剔除外部,剩下的内核部分(如图2).如果“牟盒方盖”的主视图和左视图都是圆,则其俯视图形状为下列几幅图中的( )| A. |  | B. | 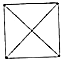 | C. | 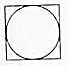 | D. | 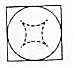 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
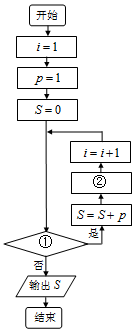 给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.
给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com