
| A. | 3πR2 | B. | 2πR2 | C. | $\frac{5π{R}^{2}}{2}$ | D. | $\frac{7π{R}^{2}}{2}$ |
分析 由题意圆柱的底面为球的截面,由球的截面性质可得出圆柱的高为h、底面半径为r与球的半径为R的关系,再用h和r表示出圆柱的侧面积,利用基本不等式求最值即可.
解答  解:如图为轴截面,令圆柱的高为h,底面半径为r,侧面积为S,
解:如图为轴截面,令圆柱的高为h,底面半径为r,侧面积为S,
则($\frac{h}{2}$)2+r2=R2,
即h=2 $\sqrt{{R}^{2}-{r}^{2}}$.
∵S=2πRh=4πr•$\sqrt{{R}^{2}-{r}^{2}}$=4π $\sqrt{{r}^{2}({R}^{2}-{r}^{2})}$≤4π $\sqrt{\frac{({r}^{2}+{R}^{2}-{r}^{2})^{2}}{4}}$=2πR2,
取等号时,内接圆柱底面半径为 $\frac{\sqrt{2}}{2}$R,高为 $\sqrt{2}$R.
圆柱的表面积为:2πR2+2π($\frac{\sqrt{2}}{2}$R)2=3πR2.
故选:A.
点评 本题考查球与圆柱的组合体问题、以及利用基本不等式求最值问题,难度一般.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
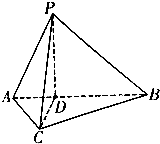 如图所示,三棱锥P-ABC中,点D为线段AB上一点,AC⊥BC,PD⊥平面ABC,AD=$\frac{1}{2}$DB,PD=BD,∠ABC=30°.
如图所示,三棱锥P-ABC中,点D为线段AB上一点,AC⊥BC,PD⊥平面ABC,AD=$\frac{1}{2}$DB,PD=BD,∠ABC=30°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 气温(℃) | 14 | 12 | 8 | 6 |
| 用电量(度) | 22 | 26 | 34 | 38 |
| A. | 60 | B. | 50 | C. | 40 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com