
Ζ÷Έω Θ®ΔώΘ©÷±Ϋ””…÷±œΏΒΡ≤Έ ΐΖΫ≥Χœϊ»Ξ≤Έ ΐtΒΟΒΫ÷±œΏΒΡΤ’Ά®ΖΫ≥ΧΘΜΑ―Β» ΫΠ―=6cosΠ»ΝΫ±ΏΆ§ ±≥Υ“‘Π―Θ§¥ζ»κx=Π―cosΠ»Θ§Π―2=x2+y2ΒΟ¥πΑΗΘΜ
Θ®ΔρΘ©Α―÷±œΏΒΡ≤Έ ΐΖΫ≥Χ¥ζ»κ‘≤ΒΡΤ’Ά®ΖΫ≥ΧΘ§άϊ”Ο÷±œΏ≤Έ ΐΖΫ≥Χ÷–≤Έ ΐtΒΡΦΗΚΈ“β“ε«σΒΟ|PA|+|PB|ΒΡ÷ΒΘ°
Ϋβ¥π ΫβΘΚΘ®ΔώΘ©÷±œΏlΒΡ≤Έ ΐΖΫ≥ΧΈΣ$\left\{\begin{array}{l}x=1-\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.$Θ®tΈΣ≤Έ ΐΘ©Θ§œϊ»Ξ≤Έ ΐΘ§
Ω…ΒΟ÷±œΏlΒΡΤ’Ά®ΖΫ≥ΧΈΣΘΚ$\sqrt{3}$x+y-$\sqrt{3}$=0 Γ≠Θ®2Ζ÷Θ©
«ζœΏCΒΡΦΪΉχ±ξΖΫ≥ΧΈΣΠ―=6cosΠ»Θ§Φ¥ Π―2=6Π―cosΠ»Θ§Μ·ΈΣ÷±Ϋ«Ήχ±ξΖΫ≥ΧΈΣ x2+y2=6xΘ§
Φ¥‘≤CΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΈΣΘΚΘ®x-3Θ©2+y2=9Γ≠Θ®5Ζ÷Θ©
Θ®ΔρΘ©Α―÷±œΏΒΡ≤Έ ΐΖΫ≥Χ¥ζ»κ‘≤CΒΡΖΫ≥ΧΘ§Μ·ΦρΒΟΘΚt2+2t-5=0Γ≠Θ®8Ζ÷Θ©
Υυ“‘Θ§t1+t2=-2Θ§t1t2=-5ΘΦ0
Υυ“‘|PA|+|PB|=|t1|+|t2|=|t1-t2|=$\sqrt{{{Θ®{{t_1}+{t_2}}Θ©}^2}-4{t_1}{t_2}}$=$2\sqrt{6}$Γ≠Θ®10Ζ÷Θ©
ΒψΤά ±ΨΧβΩΦ≤ι≤Έ ΐΖΫ≥ΧΜ·Τ’Ά®ΖΫ≥ΧΘ§ΩΦ≤ιΦΪΉχ±ξΖΫ≥ΧΜ·÷±Ϋ«Ήχ±ξΖΫ≥ΧΘ§ΩΦ≤ιΝΥ÷±œΏΒΡ≤Έ ΐΖΫ≥Χ÷–≤Έ ΐtΒΡΦΗΚΈ“β“εΘ§ «Μυ¥ΓΧβΘ°


 Οϊ ΠΒψ≤ΠΨμœΒΝ–¥πΑΗ
Οϊ ΠΒψ≤ΠΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
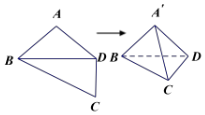 »γΆΦΘ§‘ΎΤΫΟφΥΡ±Ώ–ΈABCD÷–Θ§AB=AD=CD=1Θ§$BD=\sqrt{2}$Θ§BDΓΆCDΘ§ΫΪΤδ―ΊΕ‘Ϋ«œΏBD’έ≥…ΥΡΟφΧεAΓδ-BCDΘ§ ΙΤΫΟφAΓδBDΓΆΤΫΟφBCDΘ§»τΥΡΟφΧεAΓδ-BCDΕΞΒψ‘ΎΆ§“Μ«ρΟφ…œΘ§‘ρΗΟ«ρΒΡ±μΟφΜΐΈΣΘ®ΓΓΓΓΘ©
»γΆΦΘ§‘ΎΤΫΟφΥΡ±Ώ–ΈABCD÷–Θ§AB=AD=CD=1Θ§$BD=\sqrt{2}$Θ§BDΓΆCDΘ§ΫΪΤδ―ΊΕ‘Ϋ«œΏBD’έ≥…ΥΡΟφΧεAΓδ-BCDΘ§ ΙΤΫΟφAΓδBDΓΆΤΫΟφBCDΘ§»τΥΡΟφΧεAΓδ-BCDΕΞΒψ‘ΎΆ§“Μ«ρΟφ…œΘ§‘ρΗΟ«ρΒΡ±μΟφΜΐΈΣΘ®ΓΓΓΓΘ©| AΘ° | $\frac{{\sqrt{3}}}{2}Π–$ | BΘ° | 3Π– | CΘ° | $\frac{{\sqrt{2}}}{3}Π–$ | DΘ° | 2Π– |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 1+3i | BΘ° | -1+3i | CΘ° | 1-3i | DΘ° | -1-3i |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | »τlΓΈΠΝΘ§ΠΝΓΆΠ¬Θ§‘ρlΓΆΠ¬ | BΘ° | »τlΓΈΠΝΘ§ΠΝΓΈΠ¬Θ§‘ρlΓΈΠ¬ | CΘ° | »τlΓΆΠΝΘ§ΠΝΓΈΠ¬Θ§‘ρlΓΆΠ¬ | DΘ° | »τlΓΆΠΝΘ§ΠΝΓΆΠ¬Θ§‘ρlΓΈΠ¬ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | -1+2i | BΘ° | 1-2i | CΘ° | -1-2i | DΘ° | 1+2i |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | -4 | BΘ° | 8 | CΘ° | 11 | DΘ° | 13 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com