
分析 画出Venn图,列出关系式,计算即得结论.
解答 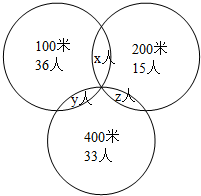 解:依题意,画出Venn图,则
解:依题意,画出Venn图,则
$\left\{\begin{array}{l}{36+15+33+x+y+z=153}\\{x=5y}\\{\frac{1}{3}z-2=y}\end{array}\right.$,
化简得:$\left\{\begin{array}{l}{x+y+z=69}\\{x=5y}\\{z=3y+6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=35}\\{y=7}\\{z=27}\end{array}\right.$,
∴参加100m和200m两项比赛的人数x=35,
故答案为:35.
点评 本题考查Venn图表达集合的关系及运算,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -20 | B. | -10 | C. | 10 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
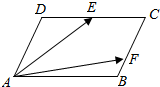 如图,平行四边形ABCD中,E为CD中点,F在线段BC上,且BC=3BF.已知$\overrightarrow{AD}$=x$\overrightarrow{AE}$+y$\overrightarrow{AF}$,则x的值为$\frac{6}{5}$.
如图,平行四边形ABCD中,E为CD中点,F在线段BC上,且BC=3BF.已知$\overrightarrow{AD}$=x$\overrightarrow{AE}$+y$\overrightarrow{AF}$,则x的值为$\frac{6}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,3,6} | B. | {1,2,3,6} | C. | {2,3,-3,6} | D. | {2,-2,3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com