
分析 (1)由题意可得f(0)=0,f(1)=-$\frac{1}{2}$,f′(1)=0,即可求得a,b,c,进而得到所求解析式;
(2)求出导数,令导数大于0,解不等式即可得到增区间.
解答 解:(1)函数f(x)=x3+ax2+bx+c(a,b为常数)的图象过原点,
可得f(0)=0,即有c=0,
又导数为f′(x)=3x2+2ax+b,
在x=1处的切线为y=-$\frac{1}{2}$,则f(1)=-$\frac{1}{2}$,f′(1)=0,
即为1+a+b=-$\frac{1}{2}$,3+2a+b=0,
解得a=-$\frac{3}{2}$,b=0,
即有f(x)=x3-$\frac{3}{2}$x2;
(2)f(x)=x3-$\frac{3}{2}$x2的导数为f′(x)=3x2-3x,
令导数f′(x)>0,可得x>1或x<0.
则函数f(x)的单调增区间为(-∞,0),(1,+∞).
点评 本题考查导数的运用:求切线的斜率和单调区间,主要考查导数的几何意义,同时考查二次不等式的解法,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在Rt△ABC内有一内接正方形,它的一条边在斜边BC上,设AB=a,∠ABC=θ,△ABC的面积为P,正方形面积为Q.求$\frac{P}{Q}$的最小值.
在Rt△ABC内有一内接正方形,它的一条边在斜边BC上,设AB=a,∠ABC=θ,△ABC的面积为P,正方形面积为Q.求$\frac{P}{Q}$的最小值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{-a{\;}^{2}-c{\;}^{2}}{c{\;}^{2}}$ | B. | $\frac{c(λ-1)}{a}$ | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
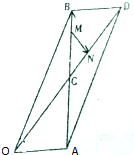 如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=6,∠AOB=60°.
如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=6,∠AOB=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com