
分析 (I)利用和差公式、倍角公式可得f(x)=$\sqrt{2}sin({2x+\frac{π}{4}})+1$,再利用正弦函数的单调性即可得出;
(II)利用正弦函数的单调性即可得出.
解答 解:(Ⅰ)$f(x)=\sqrt{2}({sin2x•\frac{{\sqrt{2}}}{2}+cos2x•\frac{{\sqrt{2}}}{2}})+1$=$\sqrt{2}({sin2x•cos\frac{π}{4}+cos2x•sin\frac{π}{4}})+1$=$\sqrt{2}sin({2x+\frac{π}{4}})+1$,
要使f(x)递减,则$2x+\frac{π}{4}$要满足:$2kπ+\frac{π}{2}≤2x+\frac{π}{4}≤2kπ+\frac{3π}{2},k∈Z$,
即$kπ+\frac{π}{8}≤x≤kπ+\frac{5π}{8},k∈Z$,
所以函数f(x)的递减区间是$[{kπ+\frac{π}{8},kπ+\frac{5π}{8}}](k∈Z)$.
(Ⅱ)因为$-\frac{π}{4}≤x≤\frac{π}{4}$,所以$-\frac{π}{4}≤2x+\frac{π}{4}≤\frac{3π}{4}$,
所以$-\frac{{\sqrt{2}}}{2}≤sin({2x+\frac{π}{4}})≤1$,
所以$-1≤\sqrt{2}sin({2x+\frac{π}{4}})≤\sqrt{2}$,
所以$0≤\sqrt{2}sin({2x+\frac{π}{4}})+1≤1+\sqrt{2}$.
故当$x∈[-\frac{π}{4},\frac{π}{4}]$时,
函数f(x)的最小值是0,此时$sin({2x+\frac{π}{4}})=-\frac{{\sqrt{2}}}{2}$,得$x=-\frac{π}{4}$;
函数f(x)的最大值是$1+\sqrt{2}$,此时$sin({2x+\frac{π}{4}})=1$,得$x=\frac{π}{8}$.
点评 本题考查了三角函数的图象与性质、倍角公式、和差公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | :?x≥-1,x2≤1 | B. | ?x<-1,x2≤1 | C. | :?x<-1,x2≤1 | D. | ?x≥-1,x2≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
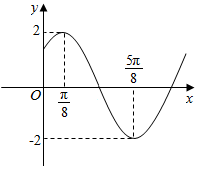 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)图象的一部分如图所示,函数g(x)=f(x+$\frac{π}{8}$),则下列结论正确的是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)图象的一部分如图所示,函数g(x)=f(x+$\frac{π}{8}$),则下列结论正确的是( )| A. | 函数g(x)的奇函数 | |
| B. | 函数f(x)与g(x)的图象均关于直线x=-$\frac{15}{8}$π对称 | |
| C. | 函数f(x)与g(x)的图象均关于点(-$\frac{π}{4}$,0)对称 | |
| D. | 函数f(x)与g(x)在区间(-$\frac{π}{3}$,0)上均单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{2}{5}$ | B. | $-\frac{4}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com