练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    不等式|x＋log3x|<|x|＋|log3x|的解集为________．


    　{x|0<x<1}

    [解析]　由对数函数定义得x>0，又由绝对值不等式的性质知，|x＋log3x|≤|x|＋|log3x|，当且仅当x与log3x同号时等号成立，∵x>0，∴log3x>0，∴x>1，故原不等式的解集为{x|0<x<1}．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图，在圆内接梯形ABCD中，AB∥DC，过点A作圆的切线与CB的延长线交于点E，若AB＝AD＝5，BE＝4，则弦BD的长为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在直角坐标系xOy中，以原点O为极点，x轴的正半轴为极轴建立极坐标系．曲线C1的参数方程为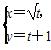(t为参数)，曲线C2的极坐标方程为ρsinθ－ρcosθ＝3，则C1与C2的交点在直角坐标系中的坐标为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    对于实数x、y，若|x－1|≤1，|y－2|≤1，则|x－2y＋1|的最大值为(　　)

    A．5　　　　                                                 B．4　　　　

    C．8　　　　                                                 D．7

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝|x－7|－|x－3|.

    (1)作出函数f(x)的图象；

    (2)当x<5时，不等式|x－8|－|x－a|>2恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a、b为正实数．

    (1)求证：＋≥a＋b；

    (2)利用(1)的结论求函数y＝(0<x<1)的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    分析法又称执果索因法，若用分析法证明：“设a>b>c，且a＋b＋c＝0，求证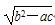<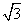a”“索”的“因”应是(　　)

    A．a－b>0                                                    B．a－c>0

    C．(a－b)(a－c)>0                                        D．(a－b)(a－c)<0

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    阅读下边的程序框图，运行相应的程序，若输入x的值为1，则输出S的值为(　　)

    A．64　　　　                                               B．73 

    C．512　　　　                                             D．585

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若＝a＋bi(a，b为实数，i为虚数单位)，则a＋b＝________.

    查看答案和解析>>

    同步练习册答案