
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 给出命题的逆否命题,结合三角函数的定义,可判断①;根据方差的意义,可判断②;根据相互独立事件概率乘法公式,可判断③;根据正态分布的对称性,可判断④.
解答 解:①中给出命题的逆否命题是“a=2kπ+$\frac{π}{2}$(k∈Z)是cosα=0的充分必要条件”,
显然当cosα=0时,a=2kπ+$\frac{π}{2}$(k∈Z),所以必要性不成立,所以命题①错误;
②方差表达了样本数据的波动大小,当一组样本数据中的每个数据都加上同一个常数,则样本的方差不变,所以②正确;
③先后抛两枚硬币,显然事件A是否发生对事件B发生的概率没有影响,所以事件A和B相互独立,
由相互独立事件概率公式可知它们同时发生的概率P(AB)=P(A)P(B)=$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{4}$,所以③正确;
④因为ξ服从正态分布N(1,σ2),其对称轴为x=1,ξ位于区域(0,1)内的概率为0.5,所以④错误,
综上所述正确的命题只有②③两个,
故选C.
点评 本题以命题的真假判断与应用为载体,考查了充要条件,四种命题,方差的意义,相互独立事件概率乘法公式,正态分布等知识点,难度中档.


 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -$\frac{1}{3}$ | C. | $\frac{29}{3}$ | D. | $\frac{29}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
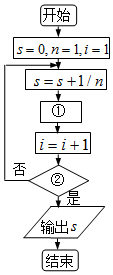 如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则图中执行框中的①处和判断框中的②处应填的语句是( )
如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则图中执行框中的①处和判断框中的②处应填的语句是( )| A. | n=n+1,i>1009 | B. | n=n+2,i>1009 | C. | n=n+1,i>1010 | D. | n=n+2,i>1010 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com