
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 对于①根据斜率公式判断即可,对于②根据函数的单调性判断即可,对于③④根据正弦函数的图象和性质判断即可
解答 解:①由于$\frac{sin{x}_{1}}{{x}_{1}}$表示直线OA的斜率,$\frac{sin{x}_{2}}{{x}_{2}}$表示直线OB的斜率,A在第三象限时,与原点连线斜率为正,B在第四象限时,与原点所连直线斜率为负,
故①不正确;
②由于函数y=sinx(-π<x<0)的单调性不确定,故由x1<x2,不能推出①sinx1<sinx2 . 故②sinx1<sinx2 ,不一定成立.
③由于函数y=sinx的图象在(-$\frac{π}{2}$,0)上是下凹型的,而$\frac{1}{2}$(sinx1+sinx2)表示线段AB中点的纵坐标,故有③$\frac{1}{2}({sin{x_1}+sin{x_2}})>sin\frac{{{x_1}+{x_2}}}{2}$;
成立.
④由题意可得-$\frac{π}{2}$<$\frac{{x}_{1}}{2}$<$\frac{{x}_{2}}{2}$<0,而函数y=sinx在(-$\frac{π}{2}$,0)上是增函数,故有sin$\frac{{x}_{1}}{2}$<sin$\frac{{x}_{2}}{2}$成立,故④不正确.
故③正确.
故选:B.
点评 本题主要正弦函数的单调性,线段的中点公式以及直线的斜率公式的应用,属于基本知识的考查.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | ln 3 | C. | $\frac{1}{3ln3}$ | D. | $\frac{1}{ln3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
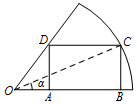 为了废物利用,准备把半径为2,圆心角为$\frac{π}{3}$的扇形铁片余料剪成如图所示的内接矩形ABCD.试用图中α表出内接矩形ABCD的面积S.
为了废物利用,准备把半径为2,圆心角为$\frac{π}{3}$的扇形铁片余料剪成如图所示的内接矩形ABCD.试用图中α表出内接矩形ABCD的面积S.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A⊆B | B. | A∪B=A | C. | A∩B=∅ | D. | A∩∁RB≠∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com