
分析 先设∠ADC=θ则可知∠ADB的大小,根据余弦定理分别可得x,y和θ的关系式,联立方程求得x的范围,即可得答案.
解答 解:设∠ADC=θ,则∠ADB=π-θ,(0<θ<π),
根据余弦定理得,
12+y2-2ycosθ=(6-x)2,①
12+y2-2ycos(π-θ)=x2.②
由①+②整理得y=$\sqrt{{x}^{2}-6x+17}$,
其中$\left\{\begin{array}{l}{x>0}\\{x+2>6-x}\\{(6-x)+2>x}\end{array}\right.$,可以解得2<x<4,
∴函数的定义域为(2,4).
点评 本题主要考查了余弦定理的应用.函数的定义域是使式子有意义的自变量的取值范围,同时也要注意变量的实际意义的要求.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{C}_{3}^{2}}{{C}_{50}^{2}}$ | B. | $\frac{{C}_{3}^{1}{C}_{47}^{1}}{{C}_{50}^{2}}$ | C. | $\frac{{C}_{47}^{2}}{{C}_{50}^{2}}$ | D. | 1-$\frac{{C}_{47}^{2}}{{C}_{50}^{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A=B | B. | B=A∪C | C. | B=A∩C | D. | B⊆C |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
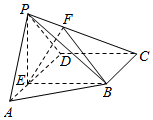 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,E为AD上一点,F为PC上一点,四边形BCDE为矩形,∠PAD=60°,PB=2$\sqrt{3}$,PA=ED=2AE=2.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,E为AD上一点,F为PC上一点,四边形BCDE为矩形,∠PAD=60°,PB=2$\sqrt{3}$,PA=ED=2AE=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com