
【题目】正方体![]() 中,
中,![]() 是棱
是棱![]() 的中点,
的中点,![]() 是侧面
是侧面![]() 上的动点,且
上的动点,且![]() 平面
平面![]() ,记
,记![]() 与
与![]() 的轨迹构成的平面为
的轨迹构成的平面为![]() .
.
①![]() ,使得
,使得![]() ;
;
②直线![]() 与直线
与直线![]() 所成角的正切值的取值范围是
所成角的正切值的取值范围是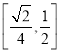 ;
;
③![]() 与平面
与平面![]() 所成锐二面角的正切值为
所成锐二面角的正切值为![]() ;
;
④正方体![]() 的各个侧面中,与
的各个侧面中,与![]() 所成的锐二面角相等的侧面共四个.
所成的锐二面角相等的侧面共四个.
其中正确命题的序号是________.(写出所有正确命题的序号)
【答案】①②③④
【解析】
取![]() 中点
中点![]() ,
,![]() 中点
中点![]() ,
,![]() 中点
中点![]() ,先利用中位线的性质判断点
,先利用中位线的性质判断点![]() 的运动轨迹为线段
的运动轨迹为线段![]() ,平面
,平面![]() 即为平面
即为平面![]() ,画出图形,再依次判断:①利用等腰三角形的性质即可判断;②直线
,画出图形,再依次判断:①利用等腰三角形的性质即可判断;②直线![]() 与直线
与直线![]() 所成角即为直线
所成角即为直线![]() 与直线
与直线![]() 所成角,设正方体的棱长为2,进而求解;③由
所成角,设正方体的棱长为2,进而求解;③由![]() ,取
,取![]() 为
为![]() 中点,则
中点,则![]() ,则
,则![]() 即为
即为![]() 与平面
与平面![]() 所成的锐二面角,进而求解;④由平行的性质及图形判断即可.
所成的锐二面角,进而求解;④由平行的性质及图形判断即可.
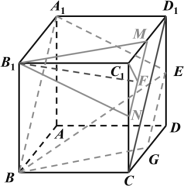
取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,所以
,所以![]() ,所以平面
,所以平面![]() 即为平面
即为平面![]() ,
,
取![]() 中点
中点![]() ,
,![]() 中点
中点![]() ,连接
,连接![]() ,则易证得
,则易证得![]() ,
,
所以平面![]() 平面
平面![]() ,所以点
,所以点![]() 的运动轨迹为线段
的运动轨迹为线段![]() ,平面
,平面![]() 即为平面
即为平面![]() .
.
①取![]() 为
为![]() 中点,因为
中点,因为![]() 是等腰三角形,所以
是等腰三角形,所以![]() ,又因为
,又因为![]() ,所以
,所以![]() ,故①正确;
,故①正确;
②直线![]() 与直线
与直线![]() 所成角即为直线
所成角即为直线![]() 与直线
与直线![]() 所成角,设正方体的棱长为2,当点
所成角,设正方体的棱长为2,当点![]() 为
为![]() 中点时,直线
中点时,直线![]() 与直线
与直线![]() 所成角最小,此时
所成角最小,此时![]() ,
,![]() ;
;
当点![]() 与点
与点![]() 或点
或点![]() 重合时,直线
重合时,直线![]() 与直线
与直线![]() 所成角最大,此时
所成角最大,此时![]() ,
,
所以直线![]() 与直线
与直线![]() 所成角的正切值的取值范围是
所成角的正切值的取值范围是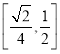 ,②正确;
,②正确;
③![]() 与平面
与平面![]() 的交线为
的交线为![]() ,且
,且![]() ,取
,取![]() 为
为![]() 中点,则
中点,则![]() 即为
即为![]() 与平面
与平面![]() 所成的锐二面角,
所成的锐二面角,![]() ,所以③正确;
,所以③正确;
④正方体![]() 的各个侧面中,平面
的各个侧面中,平面![]() ,平面
,平面![]() ,平面
,平面![]() ,平面
,平面![]() 与平面
与平面![]() 所成的角相等,所以④正确.
所成的角相等,所以④正确.
故答案为:①②③④


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,已知四边形AA1C1C为矩形,AA1=6,AB=AC=4,∠BAC=∠BAA1=60°,∠A1AC的角平分线AD交CC1于D.
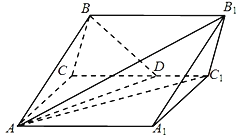
(1)求证:平面BAD⊥平面AA1C1C;
(2)求二面角A﹣B1C1﹣A1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全球抗击新冠肺炎疫情期间,我国医疗物资生产企业加班加点生产口罩、防护服、消毒水等防疫物品,保障抗疫一线医疗物资供应,在国际社会上赢得一片赞誉.我国某口罩生产企业在加大生产的同时,狠抓质量管理,不定时抽查口罩质量,该企业质检人员从所生产的口罩中随机抽取了100个,将其质量指标值分成以下六组:![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,得到如下频率分布直方图.
,得到如下频率分布直方图.
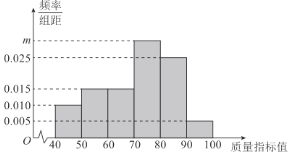
(1)求出直方图中![]() 的值;
的值;
(2)利用样本估计总体的思想,估计该企业所生产的口罩的质量指标值的平均数和中位数(同一组中的数据用该组区间中点值作代表,中位数精确到0.01);
(3)现规定:质量指标值小于70的口罩为二等品,质量指标值不小于70的口罩为一等品.利用分层抽样的方法从该企业所抽取的100个口罩中抽出5个口罩,并从中再随机抽取2个作进一步的质量分析,试求这2个口罩中恰好有1个口罩为一等品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() .
.
(1)求曲线![]() 的直角坐标方程与直线l的参数方程;
的直角坐标方程与直线l的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年全球爆发新冠肺炎,人感染了新冠肺炎病毒后常见的呼吸道症状有:发热、咳嗽、气促和呼吸困难等,严重时会危及生命.随着疫情的发展,自2020年2月5日起,武汉大面积的爆发新冠肺炎,政府为了及时收治轻症感染的群众,逐步建立起了14家方舱医院,其中武汉体育中心方舱医院从2月12日开舱至3月8日闭仓,累计收治轻症患者1056人.据部分统计该方舱医院从2月26日至3月2日轻症患者治愈出仓人数的频数表与散点图如下:
日期 | 2.26 | 2.27 | 2.28 | 2.29 | 3.1 | 3.2 |
序号 | 1 | 2 | 3 | 4 | 5 | 6 |
出仓人数 | 3 | 8 | 17 | 31 | 68 | 168 |

根据散点图和表中数据,某研究人员对出仓人数![]() 与日期序号
与日期序号![]() 进行了拟合分析.从散点图观察可得,研究人员分别用两种函数①
进行了拟合分析.从散点图观察可得,研究人员分别用两种函数①![]() ②
②![]() 分析其拟合效果.其相关指数
分析其拟合效果.其相关指数![]() 可以判断拟合效果,R2越大拟合效果越好.已知
可以判断拟合效果,R2越大拟合效果越好.已知![]() 的相关指数为
的相关指数为![]() .
.
(1)试根据相关指数判断.上述两类函数,哪一类函数的拟合效果更好?(注:相关系数![]() 与相关指数R2满足
与相关指数R2满足![]() ,参考数据表中
,参考数据表中![]() )
)
(2)①根据(1)中结论,求拟合效果更好的函数解析式;(结果保留小数点后三位)
②3月3日实际总出仓人数为216人,按①中的回归模型计算,差距有多少人?
(附:对于一组数据![]() ,其回归直线为
,其回归直线为![]()
相关系数
参考数据:
|
|
|
|
|
|
|
|
|
3.5 | 49.17 | 15.17 | 3.13 | 894.83 | 19666.83 | 10.55 | 13.56 | 3957083 |
![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周率π是数学中一个非常重要的数,历史上许多中外数学家利用各种办法对π进行了估算.现利用下列实验我们也可对圆周率进行估算.假设某校共有学生N人,让每人随机写出一对小于1的正实数a,b,再统计出a,b,1能构造锐角三角形的人数M,利用所学的有关知识,则可估计出π的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方法从该校四个年级的本科生中抽取一个容量为300的样本进行调查.已知该校一、二、三、四年级本科生人数之比为6:5:5:4,则应从一年级中抽取90名学生
B.10件产品中有7件正品,3件次品,从中任取4件,则恰好取到1件次品的概率为![]()
C.已知变量x与y正相关,且由观测数据算得![]() =3,
=3,![]() =3.5,则由该观测数据算得的线性回归方程可能是
=3.5,则由该观测数据算得的线性回归方程可能是![]() =0.4x+2.3
=0.4x+2.3
D.从装有2个红球和2个黑球的口袋内任取2个球,至少有一个黑球与至少有一个红球是两个互斥而不对立的事件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com