
分析 由已知可求范围α+$\frac{π}{4}$∈($\frac{π}{4}$,$\frac{3π}{4}$),利用同角三角函数基本关系式可求sin(α+$\frac{π}{4}$)的值,进而根据两角差的正弦函数公式,特殊角的三角函数值即可化简求值.
解答 解:∵α∈(0,$\frac{π}{2}$),且cos(α+$\frac{π}{4}$)=$\frac{5}{13}$,
∴α+$\frac{π}{4}$∈($\frac{π}{4}$,$\frac{3π}{4}$),sin(α+$\frac{π}{4}$)=$\sqrt{1-co{s}^{2}(α+\frac{π}{4})}$=$\frac{12}{13}$,
∴sinα=sin[(α+$\frac{π}{4}$)-$\frac{π}{4}$]=sin(α+$\frac{π}{4}$)cos$\frac{π}{4}$-cos(α+$\frac{π}{4}$)sin$\frac{π}{4}$=$\frac{12}{13}$×$\frac{\sqrt{2}}{2}$-$\frac{5}{13}$×$\frac{\sqrt{2}}{2}$=$\frac{{7\sqrt{2}}}{26}$.
故答案为:$\frac{{7\sqrt{2}}}{26}$.
点评 本题主要考查了同角三角函数基本关系式,两角差的正弦函数公式,特殊角的三角函数值在三角函数化简求值中的应用,属于基础题.


科目:高中数学 来源: 题型:选择题
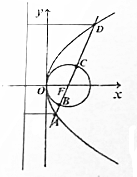 如图,抛物线:y2=4mx(m>0)和圆:x2+y2-2mx=0,直线l经过抛物线的焦点,依次交抛物线,圆于A,B,C,D四点,|AB|•|CD|=2,则m的值为( )
如图,抛物线:y2=4mx(m>0)和圆:x2+y2-2mx=0,直线l经过抛物线的焦点,依次交抛物线,圆于A,B,C,D四点,|AB|•|CD|=2,则m的值为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 179元 | B. | 199元 | C. | 219元 | D. | 239元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
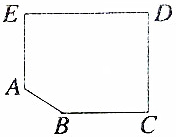 某小区内有一块荒地ABCDE,今欲在该荒地上划出一块长方形地面(不改变方位)进行开发(如图所示),问如何设计才能使开发的面积最大?最大开发面积是多少?(已知BC=210m,CD=240m,DE=300m,EA=180m)
某小区内有一块荒地ABCDE,今欲在该荒地上划出一块长方形地面(不改变方位)进行开发(如图所示),问如何设计才能使开发的面积最大?最大开发面积是多少?(已知BC=210m,CD=240m,DE=300m,EA=180m)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com