
| A. | 3x2$+\frac{\sqrt{2}}{3}{y}^{2}$=1 | B. | $\frac{{x}^{2}}{3}$$+\frac{\sqrt{2}}{3}$y2=1 | C. | $\frac{{x}^{2}}{3}$$+\sqrt{2}$y2=1 | D. | x2$+\sqrt{2}$y2=1 |
分析 设A(x1,y1),B(x2,y2),由点差法得m(x1+x2)(x1-x2)+n(y1+y2)(y1-y2)=0,设C(x0,y0),得n=$\sqrt{2}$m,椭圆mx2+$\sqrt{2}$my2=1,联立$\left\{\begin{array}{l}{m{x}^{2}+\sqrt{2}m{y}^{2}=1}\\{y=1-x}\end{array}\right.$,得($\sqrt{2}$+1)mx2-2$\sqrt{2}$mx+$\sqrt{2}$m-1=0,运用韦达定理和椭圆弦长公式能求出m,n的值,即可得到椭圆方程.
解答 解:设A(x1,y1),B(x2,y2),
将A,B点坐标代入方程得:
mx12+ny12=1,
mx22+ny22=1,
两式相减得:
m(x1+x2)(x1-x2)+n(y1+y2)(y1-y2)=0,
设AB的中点为C(x0,y0),
即有$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=2{x}_{0}}\\{{y}_{1}+{y}_{2}=2{y}_{0}}\end{array}\right.$,
mx0+ny0•$\frac{{y}_{1}-{y}_{0}}{{x}_{1}-{x}_{0}}$=0,
∴mx0+ny0kAC=0,
m=-$\frac{n{y}_{0}}{{x}_{0}}$•kAC=-n•$\frac{\sqrt{2}}{2}$•(-1)=$\frac{\sqrt{2}}{2}$n,
即n=$\sqrt{2}$m,
∴椭圆mx2+$\sqrt{2}$my2=1,
联立$\left\{\begin{array}{l}{m{x}^{2}+\sqrt{2}m{y}^{2}=1}\\{y=1-x}\end{array}\right.$,得($\sqrt{2}$+1)mx2-2$\sqrt{2}$mx+$\sqrt{2}$m-1=0,
x1+x2=$\frac{2\sqrt{2}}{\sqrt{2}+1}$,x1x2=$\frac{\sqrt{2}m-1}{(\sqrt{2}+1)m}$,
|AB|=$\sqrt{2}$$\sqrt{(\frac{2\sqrt{2}}{\sqrt{2}+1})^{2}-\frac{4(\sqrt{2}m-1)}{(\sqrt{2}+1)m}}$=2$\sqrt{2}$,
解得m=$\frac{1}{3}$,n=$\frac{\sqrt{2}}{3}$.
即有椭圆方程为$\frac{{x}^{2}}{3}$+$\frac{\sqrt{2}{y}^{2}}{3}$=1.
故选:B.
点评 本题考查椭圆方程的求法,是中档题,解题时要认真审题,注意点差法和椭圆弦长公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-3x+2=0,则x=2”的逆否命题为“若x≠2,则x2-3x+2≠0” | |
| B. | “a=3”是“函数f(x)=logax在定义域上为增函数”的充分不必要条件 | |
| C. | 若命题p:?n∈N,3n>100,则¬p:?n∈N,3n≤100 | |
| D. | 命题“?x∈(-∞,0),3x<5x”是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
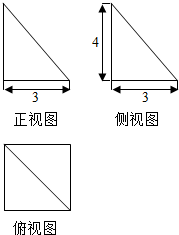
| A. | $\frac{1}{4}π$ | B. | 3π | C. | 4π | D. | $\frac{4}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0° | B. | 90° | C. | 180° | D. | 270° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{π}{4}$,$\frac{π}{4}$] | B. | [0,$\frac{π}{4}$]∪($\frac{π}{2}$,$\frac{3π}{4}$] | C. | [0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π] | D. | [$\frac{π}{4}$,$\frac{3π}{4}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com