练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．计算：log3$\frac{27}{5}$+log32-log3$\frac{6}{5}$=2．

    分析 根据对数的基本运算性质即可求出．

    解答 解：log3$\frac{27}{5}$+log32-log3$\frac{6}{5}$=log3（$\frac{27}{5}$×2×$\frac{5}{6}$）=log332=2，
    故答案为：2．

    点评 本题考查了对数的基本运算性质，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

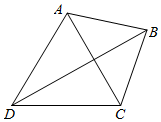    1．某学习小组进行课外研究性学习，为了测量如图所示不能到达的A、B两地，他们测得C、D两地的直线距离为2km，并用仪器测得相关角度大小分别为∠ADB=30°，∠CDB=30°，∠ACD=60°，∠ACB=45°，则A、B两地的距离大约等于（　　）（提供数据：$\sqrt{2}≈1.414，\sqrt{3}≈1.732$，结果保留两个有效数字）
    A．1.3B．1.4C．1.5D．1.6

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知函数f（x）的导函数为f′（x），且满足f（x）=5x2+3xf′（3），则f′（5）=5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

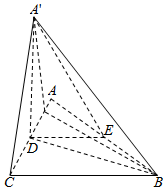    19．如图，△ABC是等腰直角三角形，∠ACB=90°，AC=2a，D，E分别为AC，AB的中点，沿DE将△ADE折起，得到四棱锥A′-BCDE，已知A′H⊥CD，垂足为H．
    （Ⅰ）求证：平面A′HB⊥平面BCDE；
    （Ⅱ）求三棱锥B-A′DE的最大体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．下面的结论：
    ①若△ABC是锐角三角形，且A为最大角，则A≥60°；
    ②已知实数a，b，“a＞1，且b＞1”等价于“a+b＞1，且ab＞1”
    ③对于任意实数a，b，式子|a+b|，|a-b|，|1-a|中至少有一个不小于$\frac{1}{2}$；
    ④设SA，SB是圆锥SO的两条母线，O是底面圆心，C是SB上一点，则AC与平面SOB不垂直．
    其中正确的有①③④（请把所有正确结论的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知k∈Z，角的终边只落在y轴正半轴上的角是（　　）
    A．$\frac{kπ}{2}$B．kπ+$\frac{π}{2}$C．2kπ+$\frac{π}{2}$D．2kπ-$\frac{π}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．定义域为R的函数f（x）满足以下条件：
    （1）对于任意x∈R，f（x）+f（-x）=0；
    （2）对于任意x1、x2∈[1，3]，当x2＞x1时，有f（x2）＞f（x1）＞0；
    则以下不等式不一定成立的是（　　）
    A．f（2）＞f（0）B．f（2）＞f（1）C．f（-3）＜f（-1）D．f（4）＞f（2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．在直角坐标系xOy中，以坐标原点为极点，x轴为极轴建立极坐标系，曲线C的参数方程为：$\left\{\begin{array}{l}{x=2cosθ}\\{y=\sqrt{2}sinθ}\end{array}\right.$（θ为参数），曲线M参数方程为：$\left\{\begin{array}{l}{x=\sqrt{2}cosθ}\\{y=\sqrt{2}sinθ}\end{array}\right.$（θ为参数）．
    （1）求曲线C、M的普通方程；
    （2）若点A在椭圆C上，点B在直线ρsinθ=2上，且OA⊥OB，求直线AB与曲线M的位置关系，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．△ABC的三个内角A、B、C的对边分别是a、b、c，其面积S=a2-（b-c）2．若a=2，则BC边上的中线长的取值范围是（1，4]．

    查看答案和解析>>

    同步练习册答案