
【题目】第十三届全国人民代表大会第二次会议和政协第十三届全国委员会第二次会议(简称两会)将分别于![]() 年
年![]() 月
月![]() 日和
日和![]() 月
月![]() 日在北京开幕.全国两会召开前夕,某网站推出两会热点大型调查,调查数据表明,网约车安全问题是百姓最为关心的热点之一,参与调查者中关注此问题的约占
日在北京开幕.全国两会召开前夕,某网站推出两会热点大型调查,调查数据表明,网约车安全问题是百姓最为关心的热点之一,参与调查者中关注此问题的约占![]() .现从参与者中随机选出
.现从参与者中随机选出![]() 人,并将这
人,并将这![]() 人按年龄分组:第
人按年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示:

(1)现在要从年龄较小的第![]() ,
,![]() ,
,![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人赠送礼品,求抽取的
人赠送礼品,求抽取的![]() 人中至少有
人中至少有![]() 人年龄在第
人年龄在第![]() 组的概率;
组的概率;
(2)若从所有参与调查的人中任意选出![]() 人,记关注网约车安全问题的人数为
人,记关注网约车安全问题的人数为![]() ,求
,求![]() 的分布列与期望;
的分布列与期望;
(3)把年龄在第![]() ,
,![]() ,
,![]() 组的人称为青少年组,年龄在第
组的人称为青少年组,年龄在第![]() ,
,![]() 组的人称为中老年组,若选出的
组的人称为中老年组,若选出的![]() 人中不关注网约车安全问题的人中老年人有
人中不关注网约车安全问题的人中老年人有![]() 人,问是否有
人,问是否有![]() 的把握认为是否关注网约车安全问题与年龄有关?附:
的把握认为是否关注网约车安全问题与年龄有关?附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
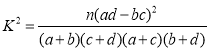 ,
,![]()
【答案】(1)![]() (2)见解析,
(2)见解析,![]() (3)没有
(3)没有
【解析】
(1)由![]() ,得
,得![]() .所以第
.所以第![]() ,
,![]() ,
,![]() 组的人数分别为
组的人数分别为![]() ,
,![]() ,
,![]() ,从第
,从第![]() ,
,![]() ,
,![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人,则第
人,则第![]() ,
,![]() ,
,![]() 组抽取的人数分别为
组抽取的人数分别为![]() ,
,![]() ,
,![]() .即可求得答案;
.即可求得答案;
(2)由题知参与调查的人中关注网约车安全问题的概率为![]() ,分别求得
,分别求得![]() ,
,![]() ,
,![]() ,
,![]() ,即可求得答案;
,即可求得答案;
(3)根据数据填写题意得![]() 列联表,求得
列联表,求得![]() ,即可求得答案.
,即可求得答案.
(1)由![]() ,得
,得![]() .
.
所以第![]() ,
,![]() ,
,![]() 组的人数分别为
组的人数分别为![]() ,
,![]() ,
,![]() ,从第
,从第![]() ,
,![]() ,
,![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人,则第
人,则第![]() ,
,![]() ,
,![]() 组抽取的人数分别为
组抽取的人数分别为![]() ,
,![]() ,
,![]() .
.
记从![]() 人中随机抽取
人中随机抽取![]() 人,至少有
人,至少有![]() 人年龄在第
人年龄在第![]() 组为事件
组为事件![]() ,则
,则![]() .
.
(2)由题知参与调查的人中关注网约车安全问题的概率为![]() ,
,
![]() 可取
可取![]() ,
,![]() ,
,![]() ,
,![]() ,且,
,且,
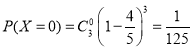 ,
,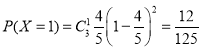 ,
,
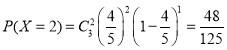 ,
,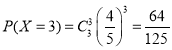
所以![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
![]() .
.
(3)由题意得![]() 列联表如下:
列联表如下:
关注网约车安全 | 不关注网约车安全 | 合计 | |
青少年 |
|
|
|
中老年 |
|
|
|
合计 |
|
|
|
![]()
所以没有![]() 的把握认为是否关注网约车安全问题与年龄有关.
的把握认为是否关注网约车安全问题与年龄有关.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】某品牌汽车4S店对最近100位采用分期付款的购车者进行统计,统计结果如下表所示:
付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
频数 | 40 | 20 |
| 10 |
|
已知分3期付款的频率为0.2,4s店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元,分2期或3期付款其利润为1.5万元,分4期或5期付款,其利润为2万元,用Y表示经销一辆汽车的利润.
(Ⅰ)求上表中![]() 的值;
的值;
(Ⅱ)若以频率作为概率,求事件![]() :“购买该品牌汽车的3位顾客中,至多有一位采用3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有一位采用3期付款”的概率![]() ;
;
(Ⅲ)求Y的分布列及数学期望EY.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.
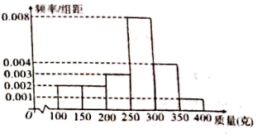
(1)经计算估计这组数据的中位数;
(2)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在
的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在![]() 内的概率.
内的概率.
(3)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有10000个,经销商提出如下两种收购方案:
A:所有芒果以10元/千克收购;
B:对质量低于250克的芒果以2元/个收购,高于或等于250克的以3元/个收购,通过计算确定种植园选择哪种方案获利更多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,长轴长为4,且过点
,长轴长为4,且过点![]() .
.
(1)求椭圆C的方程;
(2)过![]() 的直线l交椭圆C于
的直线l交椭圆C于![]() 两点,过A作x轴的垂线交椭圆C与另一点Q(Q不与
两点,过A作x轴的垂线交椭圆C与另一点Q(Q不与![]() 重合).设
重合).设![]() 的外心为G,求证
的外心为G,求证![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对称轴为坐标轴的椭圆![]() 的焦点为
的焦点为![]() ,
,![]() ,
,![]() 在
在![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设不过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且直线
两点,且直线![]() ,
,![]() ,
,![]() 的斜率依次成等比数列,则当
的斜率依次成等比数列,则当![]() 的面积为
的面积为![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 |
已知在这100人中随机抽取1人抽到喜欢游泳的学生的概率为![]() .
.
(1)请将上述列联表补充完整;
(2)并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(3)已知在被调查的学生中有5名来自甲班,其中3名喜欢游泳,现从这5名学生中随机抽取2人,求恰好有1人喜欢游泳的概率.
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: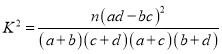 ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com