
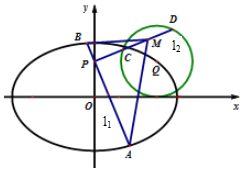
 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),圆Q(x-2)2+(y-$\sqrt{2}$)2=2的圆心Q在椭圆C上,点$P(0,\sqrt{2})$到椭圆C的右焦点的距离为$\sqrt{6}$.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),圆Q(x-2)2+(y-$\sqrt{2}$)2=2的圆心Q在椭圆C上,点$P(0,\sqrt{2})$到椭圆C的右焦点的距离为$\sqrt{6}$.分析 (1)求得圆Q的圆心,代入椭圆方程,运用两点的距离公式,解方程可得a,b的值,进而得到椭圆方程;
(2)讨论两直线的斜率不存在和为0,求得三角形MAB的面积为4;设直线y=kx+$\sqrt{2}$,代入圆Q的方程,运用韦达定理和中点坐标公式可得M的坐标,求得MP的长,再由直线AB的方程为y=-$\frac{1}{k}$x+$\sqrt{2}$,代入椭圆方程,运用韦达定理和弦长公式,由三角形的面积公式,化简整理,由换元法,结合函数的单调性,可得面积的范围.
解答 解:(Ⅰ)因为椭圆C的右焦点$F({c,0}),PF=\sqrt{6}$,
∴c=2,…1
圆Q(x-2)2+(y-$\sqrt{2}$)2=2的圆心(2,$\sqrt{2}$),
∴$(2,\sqrt{2})$在椭圆C上,代入椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1,
∴$\frac{4}{a^2}+\frac{2}{b^2}=1$,…2
由a2-b2=4
解得:a2=8,b2=4,
所以椭圆C的方程为$\frac{x^2}{8}+\frac{y^2}{4}=1$;…4
(Ⅱ)由题意可得l1的斜率不为零,当l1垂直x轴时,△MAB的面积为$\frac{1}{2}×4×2=4$,..5
当l1不垂直x轴时,设直线l1的方程为:$y=kx+\sqrt{2}$,
则直线l2的方程为:$y=-\frac{1}{k}x+\sqrt{2},A({{x_1},{y_1}}),B({{x_2},{y_2}})$,
由$\left\{\begin{array}{l}\frac{x^2}{8}+\frac{y^2}{4}=1\\ y=kx+\sqrt{2}\end{array}\right.$消去y得$({1+2{k^2}}){x^2}+4\sqrt{2}kx-4=0$,
所以${x_1}+{x_2}=\frac{{-4\sqrt{2}k}}{{1+2{k^2}}},{x_1}{x_2}=\frac{-4}{{1+2{k^2}}}$,…7
则$|{AB}|=\sqrt{1+{k^2}}|{{x_1}-{x_2}}|=\frac{{4\sqrt{(1+{k^2})(4{k^2}+1)}}}{{2{k^2}+1}}$,…8
又圆心$Q({2,\sqrt{2}})$到l2的距离${d_1}=\frac{2}{{\sqrt{1+{k^2}}}}<\sqrt{2}$得k2>1,…9
又MP⊥AB,QM⊥CD,所以M点到AB的距离等于Q点到AB的距离,设为d2,
即${d_2}=\frac{{|{2k-\sqrt{2}+\sqrt{2}}|}}{{\sqrt{1+{k^2}}}}=\frac{2|k|}{{\sqrt{1+{k^2}}}}$,…10
所以△MAB面积$s=\frac{1}{2}|{AB}|{d_2}=\frac{{4|k|\sqrt{4{k^2}+1}}}{{2{k^2}+1}}=4\sqrt{\frac{{{k^2}(4{k^2}+1)}}{{{{(2{k^2}+1)}^2}}}}$,…11
令t=2k2+1∈(3,+∞),则$\frac{1}{t}∈({0,\frac{1}{3}})$,
$S=4\sqrt{\frac{{2{t^2}-3t+1}}{{2{t^2}}}}=4\sqrt{\frac{1}{2}{{({\frac{1}{t}-\frac{3}{2}})}^2}-\frac{1}{8}}∈({\frac{{4\sqrt{5}}}{3},4})$,
综上,△MAB面积的取值范围为$({\frac{{4\sqrt{5}}}{3},4}]$…12
点评 本题考查椭圆的方程的求法,注意运用点满足椭圆方程,考查三角形的面积的范围,注意运用直线方程和椭圆方程联立,运用韦达定理和弦长公式,以及三角形的面积公式,运用换元法和函数的单调性,属于中档题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{x^2}{x}$与y=x | B. | y=$\sqrt{{x}^{2}}$与y=x | C. | y=$\root{3}{x^3}$与y=x | D. | y=${(\sqrt{x})^2}$与y=x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 0 | C. | 4 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -200 | B. | -100 | C. | 200 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{π}{16},0)$ | B. | $(\frac{π}{9},0)$ | C. | $(\frac{π}{4},0)$ | D. | $(\frac{π}{2},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,7] | B. | [0,7] | C. | [-2,7] | D. | [-2,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com