
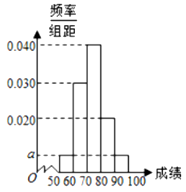
°ĺŐ‚ńŅ°Ņń≥÷į≥∆Ĺķľ∂∆ņ∂®ĽķĻĻ∂‘≤őľ”ń≥īő◊®“Ķľľ űŅľ ‘Ķń100»ňĶń≥…ľ®ĹÝ––ŃňÕ≥ľ∆£¨Ľś÷∆Ńň∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ£®»ÁÕľňý ĺ£©£¨Ļś∂®80∑÷ľį“‘…Ō’ŖĹķľ∂≥…Ļ¶£¨∑Ů‘ÚĹķľ∂ ßį‹£ģ
Ĺķľ∂≥…Ļ¶ | Ĺķľ∂ ßį‹ | ļŌľ∆ | |
ń– | 16 | ||
Ňģ | 50 | ||
ļŌľ∆ |
£®1£©«ůÕľ÷–![]() Ķń÷Ķ£Ľ
Ķń÷Ķ£Ľ
£®2£©łý囓—÷™ŐűľĢÕÍ≥…Ō¬√ś![]() Ń–Ń™ĪŪ£¨≤ĘŇ–∂Ōń‹∑Ů”–
Ń–Ń™ĪŪ£¨≤ĘŇ–∂Ōń‹∑Ů”–![]() Ķńį—ő’»Ōő™°įĹķľ∂≥…Ļ¶°Ī”Ž–‘Īū”–Ļō£Ņ
Ķńį—ő’»Ōő™°įĹķľ∂≥…Ļ¶°Ī”Ž–‘Īū”–Ļō£Ņ
£®3£©Ĺę∆Ķ¬ ”ő™łŇ¬ £¨ī”ĪĺīőŅľ ‘Ķńňý”–»ň‘Ī÷–£¨ňśĽķ≥ť»°4»ňĹÝ––‘ľŐł£¨ľ«’‚4»ň÷–Ĺķľ∂ ßį‹Ķń»ň żő™![]() £¨«ů
£¨«ů![]() Ķń∑÷≤ľŃ–”Ž ż—ß∆ŕÕŻ
Ķń∑÷≤ľŃ–”Ž ż—ß∆ŕÕŻ![]() £ģ
£ģ
£®≤őŅľĻę Ĺ£ļ![]() £¨∆š÷–
£¨∆š÷–![]() £©
£©
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
°ĺīūįł°Ņ(1) ![]() £Ľ(2)Ń–Ń™ĪŪľŻĹ‚őŲ£¨”–≥¨Ļż
£Ľ(2)Ń–Ń™ĪŪľŻĹ‚őŲ£¨”–≥¨Ļż![]() Ķńį—ő’»Ōő™°įĹķľ∂≥…Ļ¶°Ī”Ž–‘Īū”–Ļō£Ľ(3)∑÷≤ľŃ–ľŻĹ‚őŲ£¨
Ķńį—ő’»Ōő™°įĹķľ∂≥…Ļ¶°Ī”Ž–‘Īū”–Ļō£Ľ(3)∑÷≤ľŃ–ľŻĹ‚őŲ£¨![]() =3
=3
°ĺĹ‚őŲ°Ņ
£®1£©”…∆Ķ¬ ļÕő™1£¨Ń–≥Ų∑Ĺ≥Ő«ů![]() Ķń÷Ķ£Ľ
Ķń÷Ķ£Ľ
£®2£©”…∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ«ů≥ŲĹķľ∂≥…Ļ¶Ķń∆Ķ¬ £¨ľ∆ň„Ĺķľ∂≥…Ļ¶Ķń»ň ż£¨
ŐÓ–ī![]() Ń–Ń™ĪŪ£¨ľ∆ň„ĻŘ≤‚÷Ķ£¨∂‘’’ŃŔĹÁ÷ĶĶ√≥ŲĹŠ¬Ř£Ľ
Ń–Ń™ĪŪ£¨ľ∆ň„ĻŘ≤‚÷Ķ£¨∂‘’’ŃŔĹÁ÷ĶĶ√≥ŲĹŠ¬Ř£Ľ
£®3£©”…∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ÷™Ĺķľ∂ ßį‹Ķń∆Ķ¬ £¨Ĺę∆Ķ¬ ”ő™łŇ¬ £¨
÷™ňśĽķĪšŃŅ![]() ∑Ģī”∂ĢŌÓ∑÷≤ľ£¨ľ∆ň„∂‘”¶ĶńłŇ¬ ÷Ķ£¨–ī≥Ų∑÷≤ľŃ–£¨ľ∆ň„ ż—ß∆ŕÕŻ.
∑Ģī”∂ĢŌÓ∑÷≤ľ£¨ľ∆ň„∂‘”¶ĶńłŇ¬ ÷Ķ£¨–ī≥Ų∑÷≤ľŃ–£¨ľ∆ň„ ż—ß∆ŕÕŻ.
Ĺ‚£ļ£®1£©”…∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľłų–°≥§∑Ĺ–ő√śĽż◊‹ļÕő™1£¨
Ņ…÷™![]() £¨
£¨
Ĺ‚Ķ√![]() £Ľ
£Ľ
£®2£©”…∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ÷™£¨Ĺķľ∂≥…Ļ¶Ķń∆Ķ¬ ő™![]() £¨
£¨
ňý“‘Ĺķľ∂≥…Ļ¶Ķń»ň żő™![]() £®»ň£©£¨
£®»ň£©£¨
ŐÓĪŪ»ÁŌ¬£ļ
Ĺķľ∂≥…Ļ¶ | Ĺķľ∂ ßį‹ | ļŌľ∆ | |
ń– | 16 | 34 | 50 |
Ňģ | 9 | 41 | 50 |
ļŌľ∆ | 25 | 75 | 100 |
ľŔ…Ť°įĹķľ∂≥…Ļ¶°Ī”Ž–‘ĪūőřĻō£¨
łýĺ›…ŌĪŪ żĺ›īķ»ŽĻę ĹŅ…Ķ√![]() £¨
£¨
ňý“‘”–≥¨Ļż![]() Ķńį—ő’»Ōő™°įĹķľ∂≥…Ļ¶°Ī”Ž–‘Īū”–Ļō£Ľ
Ķńį—ő’»Ōő™°įĹķľ∂≥…Ļ¶°Ī”Ž–‘Īū”–Ļō£Ľ
£®3£©”…∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ÷™Ĺķľ∂ ßį‹Ķń∆Ķ¬ ő™![]() £¨
£¨
Ĺę∆Ķ¬ ”ő™łŇ¬ £¨
‘Úī”ĪĺīőŅľ ‘Ķńňý”–»ň‘Ī÷–£¨ňśĽķ≥ť»°1»ňĹÝ––‘ľŐł£¨’‚»ňĹķľ∂ ßį‹ĶńłŇ¬ ő™0.75£¨
ňý“‘![]() Ņ… ”ő™∑Ģī”∂ĢŌÓ∑÷≤ľ£¨ľī
Ņ… ”ő™∑Ģī”∂ĢŌÓ∑÷≤ľ£¨ľī![]() £¨
£¨
![]()
![]() £¨
£¨
Ļ ![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨
![]() .
.
ňý“‘![]() Ķń∑÷≤ľŃ–ő™£ļ
Ķń∑÷≤ľŃ–ő™£ļ
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
ż—ß∆ŕÕŻő™![]() .ĽÚ£®
.ĽÚ£®![]() £©£ģ
£©£ģ



| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ļĮ ż![]() «∂®“Ś‘ŕR…ŌĶń∆śļĮ ż£¨ĶĪ
«∂®“Ś‘ŕR…ŌĶń∆śļĮ ż£¨ĶĪ![]() Ī£¨
Ī£¨![]() £¨łÝ≥ŲŌ¬Ń–√ŁŐ‚£ļ
£¨łÝ≥ŲŌ¬Ń–√ŁŐ‚£ļ
ĘŔĶĪ![]() Ī£¨
Ī£¨![]() £Ľ
£Ľ
ĘŕļĮ ż![]() ”–2łŲŃ„Ķ„£Ľ
”–2łŲŃ„Ķ„£Ľ
ĘŘ![]() ĶńĹ‚ľĮő™
ĶńĹ‚ľĮő™![]() £Ľ
£Ľ
Ę‹![]() £¨
£¨![]() £¨∂ľ”–
£¨∂ľ”–![]() .
.
∆š÷–’ś√ŁŐ‚ĶńłŲ żő™£® £©
A.4B.3C.2D.1
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™Õ÷‘≤![]() Ķń◊ů”“ĹĻĶ„∑÷Īūő™
Ķń◊ů”“ĹĻĶ„∑÷Īūő™![]() ļÕ
ļÕ![]() £¨”…4łŲĶ„
£¨”…4łŲĶ„![]() °Ę
°Ę![]() °Ę
°Ę![]() ļÕ
ļÕ![]() ◊ť≥…Ńň“ĽłŲłŖő™
◊ť≥…Ńň“ĽłŲłŖő™![]() £¨√śĽżő™
£¨√śĽżő™![]() ĶńĶ»—ŁŐ›–ő£ģ
ĶńĶ»—ŁŐ›–ő£ģ
£®1£©«ůÕ÷‘≤Ķń∑Ĺ≥Ő£Ľ
£®2£©ĻżĶ„![]() Ķń÷ĪŌŖļÕÕ÷‘≤ĹĽ”ŕŃĹĶ„
Ķń÷ĪŌŖļÕÕ÷‘≤ĹĽ”ŕŃĹĶ„![]() °Ę
°Ę![]() £¨«ů
£¨«ů![]() √śĽżĶń◊Óīů÷Ķ£ģ
√śĽżĶń◊Óīů÷Ķ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ň√«ňś◊Ň…ķĽÓňģ∆ĹĶńŐŠłŖ£¨Ĺ°ŅĶ“‚ ∂÷ū≤Ĺľ”«Ņ£¨Ĺ°…ŪŅ™ ľ◊ŖĹÝ»ň√«…ķĽÓ£¨‘ŕĹ°…Ū∑Ĺ√śÕ∂»Ž‘Ĺņī‘Ĺ∂ŗ£¨ő™ŃňĶų≤ť≤ő”ŽĹ°…ŪĶńńÍ«Š»ň“ĽńÍĹ°…ŪĶńĽ®∑—«ťŅŲ£¨—–ĺŅ»ň‘Ī‘ŕ![]() Ķō«ÝňśĽķ≥ť»°Ńň≤őľ”Ĺ°…ŪĶń«ŗńÍń––‘°ĘŇģ–‘łų50√Ż£¨Ĺę∆šĽ®∑—Õ≥ľ∆«ťŅŲ»ÁŌ¬ĪŪňý ĺ£ļ
Ķō«ÝňśĽķ≥ť»°Ńň≤őľ”Ĺ°…ŪĶń«ŗńÍń––‘°ĘŇģ–‘łų50√Ż£¨Ĺę∆šĽ®∑—Õ≥ľ∆«ťŅŲ»ÁŌ¬ĪŪňý ĺ£ļ
∑÷◊ť£®Ľ®∑—£© | ∆Ķ ż |
| 6 |
| 22 |
| 25 |
| 35 |
| 8 |
| 4 |
ń––‘ | Ňģ–‘ | ļŌľ∆ | |
Ĺ°…ŪĽ®∑—≤Ľ≥¨Ļż2400‘™ | 23 | ||
Ĺ°…ŪĽ®∑—≥¨Ļż2400‘™ | 20 | ||
ļŌľ∆ |
£®1£©ÕÍ…∆∂ĢŃ™ĪŪ÷–Ķń żĺ›£Ľ
£®2£©łýĺ›ĪŪ÷–Ķń żĺ›«ťŅŲ£¨Ň–∂Ō «∑Ů”–99%Ķńį—ő’»Ōő™Ĺ°…ŪĶńĽ®∑—≥¨Ļż2400‘™”Ž–‘Īū”–Ļō£Ľ
£®3£©«ů’‚100√ŻĪĽĶų≤ť’Ŗ“ĽńÍĹ°…ŪĶń∆ĹĺýĽ®∑—£®Õ¨“Ľ◊ť żĺ›”√ł√«ÝľšĶń÷–Ķ„÷ĶīķŐś£©.
łĹ£ļ![]()
P(K2°›k) | 0.10 | 0.05 | 0.025 | 0.01 |
k | 2.706 | 3.841 | 5.024 | 6.635 |
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»Ű∂‘»ő“‚Ķń Ķ żk£¨b£¨ļĮ ż![]() ”Ž÷ĪŌŖ
”Ž÷ĪŌŖ![]() ◊‹Ōŗ«–£¨‘Ú≥∆ļĮ ż
◊‹Ōŗ«–£¨‘Ú≥∆ļĮ ż![]() ő™°įļ„«–ļĮ ż°Ī.
ő™°įļ„«–ļĮ ż°Ī.
£®1£©Ň–∂ŌļĮ ż![]() «∑Ůő™°įļ„«–ļĮ ż°Ī£Ľ
«∑Ůő™°įļ„«–ļĮ ż°Ī£Ľ
£®2£©»ŰļĮ ż![]() «°įļ„«–ļĮ ż°Ī£¨«ů Ķ żm£¨n¬ķ◊„ĶńĻōŌĶ Ĺ£Ľ
«°įļ„«–ļĮ ż°Ī£¨«ů Ķ żm£¨n¬ķ◊„ĶńĻōŌĶ Ĺ£Ľ
£®3£©»ŰļĮ ż![]() «°įļ„«–ļĮ ż°Ī£¨«ů÷§£ļ
«°įļ„«–ļĮ ż°Ī£¨«ů÷§£ļ![]() .
.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕ÷ĪĹ«◊ÝĪÍŌĶxOy÷–£¨“—÷™÷ĪŌŖlĻżĶ„P£®2£¨2£©.“‘◊ÝĪÍ‘≠Ķ„ő™ľęĶ„£¨x÷Š’żįŽ÷Šő™ľę÷ŠĹ®ŃĘľę◊ÝĪÍŌĶ£¨«ķŌŖCĶńľę◊ÝĪÍ∑Ĺ≥Őő™¶—©Ā¶—cos2¶»©Ā4cos¶»£Ĺ0.
£®1£©«ůCĶń÷ĪĹ«◊ÝĪÍ∑Ĺ≥Ő£Ľ
£®2£©»Űl”ŽCĹĽ”ŕA£¨BŃĹĶ„£¨«ů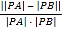 Ķń◊Óīů÷Ķ.
Ķń◊Óīů÷Ķ.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
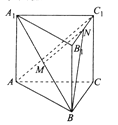
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ÷Ī»żņ‚÷ý![]() ÷–£¨
÷–£¨ ![]() ∑÷Īū «
∑÷Īū «![]() Ķń÷–Ķ„.
Ķń÷–Ķ„.
£®1£©«ů÷§£ļ ![]() ∆Ĺ√ś
∆Ĺ√ś![]() £Ľ
£Ľ
£®2£©»Ű»żņ‚÷ý![]() ĶńŐŚĽżő™4£¨«ů“ž√ś÷ĪŌŖ
ĶńŐŚĽżő™4£¨«ů“ž√ś÷ĪŌŖ![]() ”Ž
”Ž![]() ľ–Ĺ«Ķń”ŗŌ“÷Ķ.
ľ–Ĺ«Ķń”ŗŌ“÷Ķ.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ…ŤļĮ ż![]() £¨∆š÷–
£¨∆š÷–![]() ő™◊‘»Ľ∂‘ żĶńĶ◊ ż.
ő™◊‘»Ľ∂‘ żĶńĶ◊ ż.
£®1£©ĶĪ![]() Ī£¨Ň–∂ŌļĮ ż
Ī£¨Ň–∂ŌļĮ ż![]() ĶńĶ•Ķų–‘£Ľ
ĶńĶ•Ķų–‘£Ľ
£®2£©»Ű÷ĪŌŖ![]() «ļĮ ż
«ļĮ ż![]() Ķń«–ŌŖ£¨«ů Ķ ż
Ķń«–ŌŖ£¨«ů Ķ ż![]() Ķń÷Ķ£Ľ
Ķń÷Ķ£Ľ
£®3£©ĶĪ![]() Ī£¨÷§√ų£ļ
Ī£¨÷§√ų£ļ![]() .
.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨»żņ‚◊∂![]() ÷–£¨Ķ„
÷–£¨Ķ„![]() ‘ŕ“‘
‘ŕ“‘![]() ő™÷Īĺ∂Ķń‘≤
ő™÷Īĺ∂Ķń‘≤![]() …Ō£¨∆Ĺ√ś
…Ō£¨∆Ĺ√ś![]() ∆Ĺ√ś
∆Ĺ√ś![]() £¨Ķ„
£¨Ķ„![]() ‘ŕŌŖ∂ő
‘ŕŌŖ∂ő![]() …Ō£¨«“
…Ō£¨«“![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨Ķ„
£¨Ķ„![]() ő™
ő™![]() Ķń÷ō–ń£¨Ķ„
Ķń÷ō–ń£¨Ķ„![]() ő™
ő™![]() Ķń÷–Ķ„.
Ķń÷–Ķ„.

£®1£©«ů÷§£ļ![]() ∆Ĺ√ś
∆Ĺ√ś![]() £Ľ
£Ľ
£®2£©«ůĶ„![]() ĶĹ∆Ĺ√ś
ĶĹ∆Ĺ√ś![]() ĶńĺŗņŽ.
ĶńĺŗņŽ.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com