
【题目】已知函数f(x)=ex﹣![]() 有两个极值点.
有两个极值点.
(1)求实数a的取值范围;
(2)若函数f(x)的两个极值点分别为x1,x2,求证:x1+x2>2.
【答案】(1)(e,+∞);(2)见解析
【解析】
(1)f′(x)=ex﹣ax.函数f(x)=ex![]() 有两个极值点f′(x)=ex﹣ax=0有两个实数根.x=0时不满足上述方程,方程化为:a
有两个极值点f′(x)=ex﹣ax=0有两个实数根.x=0时不满足上述方程,方程化为:a![]() ,令g(x)
,令g(x)![]() ,(x≠0).利用导数已经其单调性即可得出.
,(x≠0).利用导数已经其单调性即可得出.
(2)由(1)可知:a>e时,函数f(x)有两个极值点分别为![]() ,x2,不妨设
,x2,不妨设![]() <
<![]() ,
,![]() +
+![]() >2
>2![]() >2﹣
>2﹣![]() >1
>1![]() ,由
,由![]() ,因此即证明:
,因此即证明:![]() .构造函数h(x)
.构造函数h(x)![]() ,0<x<1,2﹣x>1.利用导数已经其单调性即可得出.
,0<x<1,2﹣x>1.利用导数已经其单调性即可得出.
(1)解:f′(x)=ex﹣ax.
∵函数f(x)=ex![]() 有两个极值点.
有两个极值点.
∴f′(x)=ex﹣ax=0有两个实数根.
x=0时不满足上述方程,
方程化为:a![]() ,
,
令g(x)![]() ,(x≠0).
,(x≠0).
g′(x)![]() ,
,
可得:x<0时,g′(x)<0,函数g(x)单调递减;0<x<1时,g′(x)<0,函数g(x)单调递减;x>1时,g′(x)>0,函数g(x)单调递增.
g(1)=e,得到函数草图如图所示.
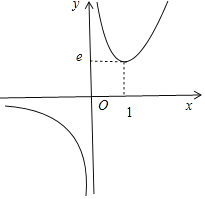
a>e时,方程f′(x)=ex﹣ax=0有两个实数根.
∴实数a的取值范围是(e,+∞).
(2)证明:由(1)可知:a>e时,函数f(x)有两个极值点分别为x1,x2,不妨设x1<x2.
证明:![]() +
+![]() >2
>2![]() >2﹣
>2﹣![]() >1
>1![]() ,
,
由![]() ,因此即证明:
,因此即证明:![]() .
.
构造函数h(x)![]() ,0<x<1,2﹣x>1.
,0<x<1,2﹣x>1.
h′(x)![]() (x﹣1)
(x﹣1)![]() ,
,
令函数u(x)![]() ,(0<x<2).
,(0<x<2).
u′(x)![]() .
.
可得函数u(x)在(0,2)内单调递减,于是函数v(x)![]() 在(0,1)内单调递减.
在(0,1)内单调递减.
v(x)≥v(1)=0.∴h′(x)![]() (x﹣1)
(x﹣1)![]() ,h(x)在(0,1)内单调递减.
,h(x)在(0,1)内单调递减.
∴h(x)>h(1)=0,
∴![]() .
.
因此![]() +
+![]() >2成立.
>2成立.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】设F1,F2分别是椭圆![]() 的左、右焦点,过
的左、右焦点,过![]() 的直线
的直线![]() 与
与![]() 相交 于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.
相交 于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.
(1)求|AB|;
(2)若直线![]() 的斜率为1,求实数
的斜率为1,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果对定义在R上的奇函数y=f(x),对任意两个不相邻的实数x1,x2,所有x1f(x1)+x2f(x2)>x1f(x2)+x2f(x1),则称函数y=f(x)为“H函数”,下列函数为H函数的是( )
A. f(x)=sinxB. f(x)=exC. f(x)=x3﹣3xD. f(x)=x|x|
查看答案和解析>>
科目:高中数学 来源: 题型:
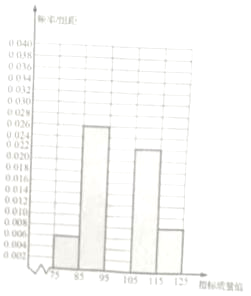
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值.由测量表得到如下频率分布直方图
(1)补全上面的频率分布直方图(用阴影表示);
(2)统计方法中,同一组数据常用该组区间的中间值作为代表,据此估计这种产品质量指标值服从正态分布Z(μ,σ2),其中μ近似为样本平均值![]() ,σ2近似为样本方差s2(组数据取中间值);
,σ2近似为样本方差s2(组数据取中间值);
①利用该正态分布,求从该厂生产的产品中任取一件,该产品为合格品的概率;
②该企业每年生产这种产品10万件,生产一件合格品利润10元,生产一件不合格品亏损20元,则该企业的年利润是多少?
参考数据:![]() =5.1,若Z~N(μ,σ2),则P(μ﹣σ,μ+σ)=0.6826,P(μ﹣2σ,μ+2σ)=0.9544.
=5.1,若Z~N(μ,σ2),则P(μ﹣σ,μ+σ)=0.6826,P(μ﹣2σ,μ+2σ)=0.9544.
查看答案和解析>>
科目:高中数学 来源: 题型:
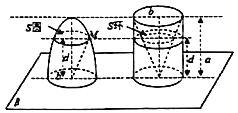
【题目】我国齐梁时代的数学家祖暅提出了一条原理:“幂势既同,则积不容异”.意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.椭球体是椭圆绕其轴旋转所成的旋转体.如图,将底面直径都为![]() ,高皆为
,高皆为![]() 的椭半球体和已被挖去了圆锥体的圆柱放置于同一平面
的椭半球体和已被挖去了圆锥体的圆柱放置于同一平面![]() 上,用平行于平面
上,用平行于平面![]() 且与平面
且与平面![]() 任意距离
任意距离![]() 处的平面截这两个几何体,可横截得到
处的平面截这两个几何体,可横截得到![]() 及
及![]() 两截面.可以证明
两截面.可以证明![]() 总成立.据此,半短轴长为1,半长轴长为3的椭球体的体积是_______.
总成立.据此,半短轴长为1,半长轴长为3的椭球体的体积是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|x2-3x+2=0},B={x|x2+(a-1)x+a2-5=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com