【题目】如图,在长方体
、
分别是棱AB、BC的中点.
(1)证明
四点共面；
(2)直线
与平面
所成角的大小.
【答案】（1）见解析；（2）
【解析】
（1）连接AC，证明EF∥AC，推出EF∥A1C1，即可证明A1、C1、F、E四点共面；（2）以D为坐标原点，DA、DC、DD1分别为xyz轴，建立空间直角坐标系，易求得
，求出平面
的法向量，利用空间向量的数量积求解直线CD1与平面A1C1FE所成的角的正弦函数值，进而可得到角．
（1）连接AC，因为E，F分别是AB，BC的中点，
所以EF是△ABC的中位线，所以EF∥AC，
由长方体的性质知AC∥A1C1，所以EF∥A1C1，
所以A1、C1、F、E四点共面．
（2）以D为坐标原点，DA、DC、DD1分别为xyz轴，建立空间直角坐标系，
则
，
，
，
，
易求得，
，
，
设平面的法向量为
，
则
，即
，
，得
，
，
所以
，所以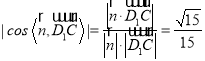
，
所以直线
与平面所成的角的正弦函数值为
，
故直线与平面
所成角的大小为.
科目：高中数学 来源： 题型：
【题目】为了提高职工的工作积极性，在工资不变的情况下，某企业给职工两种追加奖励性绩效奖金的方案:第一种方案 是每年年末(12月底)追加绩效奖金一次，第一年末追加的绩效奖金为
万元，以后每次所追加的绩效奖金比上次所追加的绩效奖金多万元;第二种方案是每半年(6月底和12月底)各追加绩效奖金一次，第一年的6月底追加的绩效奖金为
万元，以后每次所追加的绩效奖金比上次所追加的绩效奖金多万元.
假设你准备在该企业工作
年，根据上述方案，试问:
(1)如果你在该公司只工作2年，你将选择哪一种追加绩效奖金的方案?请说明理由.
(2)如果选择第二种追加绩效奖金的方案比选择第一种方案的奖金总额多，你至少在该企业工作几年?
(3)如果把第二种方案中的每半年追加万元改成每半年追加
万元，那么在什么范围内取值时，选择第二种方案的绩效奖金总额总是比选择第一种方案多?
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知等差数列
的前
项和为
，
，公差为
.
（1）若
，求数列的通项公式；
（2）是否存在
，使
成立？若存在，试找出所有满足条件的，的值，并求出数列的通项公式；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知平面直角坐标系内的动点P到直线
的距离与到点
的距离比为
．
（1）求动点P所在曲线E的方程；
（2）设点Q为曲线E与
轴正半轴的交点，过坐标原点O作直线
，与曲线E相交于异于点
的不同两点
，点C满足
，直线
和
分别与以C为圆心，
为半径的圆相交于点A和点B，求△QAC与△QBC的面积之比
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】艾滋病是一种危害性极大的传染病，由感染艾滋病病毒
病毒
引起，它把人体免疫系统中最重要的CD4T淋巴细胞作为主要攻击目标，使人体丧失免疫功能
下表是近八年来我国艾滋病病毒感染人数统计表：
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
感染者人数 |
|
|
|
|
|
|
| 85 |
请根据该统计表，画出这八年我国艾滋病病毒感染人数的折线图；
请用相关系数说明：能用线性回归模型拟合y与x的关系；
建立y关于x的回归方程
系数精确到
，预测2019年我国艾滋病病毒感染人数．
参考数据：
；
，
，
，
参考公式：相关系数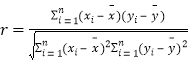
，
回归方程
中，
，
．
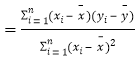查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出下列四个命题：
（1）任意两个复数都不能比较大小；（2）
为实数
为实数；（3）虚轴上的点对应的复数都是纯虚数；（4）复数集与复平面内的所有点所成的集合是一一对应的.
其中正确命题的个数是（ ）
A.1B.2C.3D.4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某科技创新公司在第一年年初购买了一台价值昂贵的设备，该设备的第1年的维护费支出为20万元，从第2年到第6年，每年的维修费增加4万元，从第7年开始，每年维修费为上一年的125%．
（1）求第n年该设备的维修费
的表达式；
（2）设
，若
万元，则该设备继续使用，否则须在第n年对设备更新，求在第几年必须对该设备进行更新？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
