Question

16．将圆心角为α的扇形卷成一个圆锥，当圆锥的体积最大时，α=$\frac{2\sqrt{6}}{3}$π．

Answer 1

分析 设圆锥的底面半径为r，高为h，体积为V，求出r²+h²=R²，表示出体积表达式，利用导数求出函数的最大值，得到结果．

解答 解：设圆锥的底面半径为r，高为h，体积为V，那么r²+h²=R²，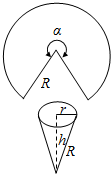

因此，V=$\frac{1}{3}$πr²h=$\frac{1}{3}$π（R²-h²）h=$\frac{1}{3}$πR²h-$\frac{1}{3}$πh³（0＜h＜R）．
V′=$\frac{1}{3}$πR²-πh²．
令V'=0，即$\frac{1}{3}$πR²-πh²=0，得 h=$\frac{\sqrt{3}}{3}$R．…（5分）
当 0＜h＜$\frac{\sqrt{3}}{3}$R时，V'＞0．
当$\frac{\sqrt{3}}{3}$R＜h＜R时，V'＜0．
所以，h=$\frac{\sqrt{3}}{3}$R时，V取得极大值，并且这个极大值是最大值．
把 h=$\frac{\sqrt{3}}{3}$R代入r²+h²=R²，得 r=$\frac{\sqrt{6}}{3}$R．
由Rα=2πr，得α=$\frac{2\sqrt{6}}{3}$π．
故答案为：$\frac{2\sqrt{6}}{3}$π．

点评 本题考查圆锥与扇形展开图的关系，体积的计算，考查计算能力，导数的应用，解题的关键是建立起体积的函数模型，理解函数的单调性与最值的关系是解本题的重点．