
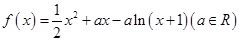 .
.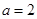 时,求函数
时,求函数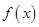 的极值;
的极值;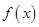 的单调区间.
的单调区间.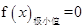 ,无极大值;(2)见解析.
,无极大值;(2)见解析.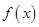 的定义域,在定义域内进行作答,在条件
的定义域,在定义域内进行作答,在条件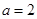 下求出函数
下求出函数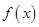 的导函数,根据函数的单调性与导数的关系,判断函数
的导函数,根据函数的单调性与导数的关系,判断函数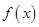 的极值;(2)先求出函数
的极值;(2)先求出函数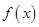 的导函数,其导函数中含有参数
的导函数,其导函数中含有参数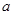 ,所以要进行分类讨论,对
,所以要进行分类讨论,对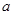 分三种情况
分三种情况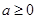 ,
,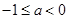 ,
,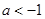 进行讨论,分别求出每种情况下的函数
进行讨论,分别求出每种情况下的函数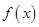 的单调增区间和单调减区间.
的单调增区间和单调减区间.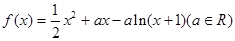 的定义域是
的定义域是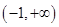 , 1分
, 1分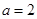 时,
时,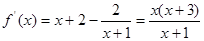 ,
,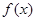 在
在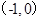 上递减,在
上递减,在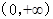 上递增,
上递增,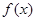 的极小值为
的极小值为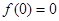 ,无极大值; 4分
,无极大值; 4分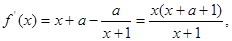 定义域
定义域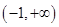 , 5分
, 5分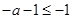 ,即
,即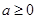 时,由
时,由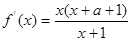
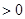 ,得
,得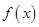 的增区间为
的增区间为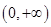 ;由
;由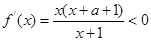 ,得
,得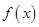 的减区间为
的减区间为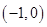 ; 7分
; 7分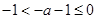 ,即
,即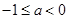 时,由
时,由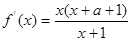
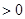 ,得
,得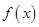 的增区间为
的增区间为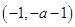 和
和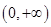 ;由
;由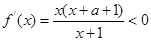 ,得
,得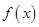 的减区间为
的减区间为 ; 9分
; 9分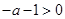 ,即
,即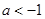 时,由
时,由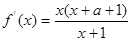
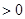 ,得
,得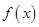 的增区间为
的增区间为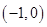 和
和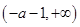 ;由
;由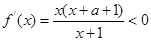 ,得
,得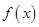 的减区间为
的减区间为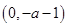 ; 11分
; 11分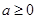 时,
时,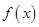 的增区间为
的增区间为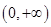 ,减区间为
,减区间为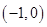 ;
;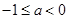 时,
时,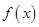 的增区间为
的增区间为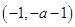 和
和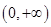 ,减区间为
,减区间为 ;
;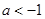 时,
时,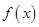 的增区间为
的增区间为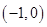 和
和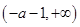 ,减区间为
,减区间为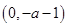 . 13分
. 13分

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com