考点:直线与圆锥曲线的关系,平面向量数量积的运算,圆的标准方程,椭圆的标准方程
专题:综合题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)由题意得c=1,a
2=2,可得椭圆C的方程;
(2)先求出点Q的坐标,再利用待定系数法,即可求过P、Q、F
2三点的圆的方程;
(3)利用
=λ,结合向量的数量积公式,结合基本不等式,即可求
•的最大值.
解答:
解:(1)由题意得c=1,a
2=2…(2分)
故椭圆的方程为
+y2=1.…(3分)
(2)因为P(0,1),F
1(-1,0),所以PF
1的方程为x-y+1=0
由
,解得点Q的坐标为
(-,-). …(5分)
设过P,Q,F
2三点的圆为x
2+y
2+Dx+Ey+F=0…(6分)
则
解得
D=,E=,F=-所以圆的方程为
x2+y2+x+y-=0…(8分)
(3)设P(x
1,y
1),Q(x
2,y
2),则
=(x1+1,y1),
=(-1-x2,-y2)因为
=λ,所以
,即
所以
,解得
x2=…(10分)
所以
•=x1x2+y1y2=x2(-λx2-λ-1)-λ=--(1+λ)x2-λ=
-()2-(1+λ)•-λ=-(λ+)…(12分)
因为
λ∈[,2],所以
λ+≥2,当且仅当
λ=,
即λ=1时,取等号.
•最大值为
. …(14分)
点评:本题考查椭圆的方程,考查圆的方程,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.



 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案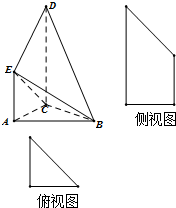 如图是某直三棱柱(侧棱与底面垂直)被削去一部分后的直观图与三视图中的侧(左)视图、俯视图,侧(左)视图是底边长分别为2和4的直角梯形,俯视图是直角边长为2的等腰直角三角形.
如图是某直三棱柱(侧棱与底面垂直)被削去一部分后的直观图与三视图中的侧(左)视图、俯视图,侧(左)视图是底边长分别为2和4的直角梯形,俯视图是直角边长为2的等腰直角三角形.