练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，AB是⊙O的直径，VA垂直于⊙O所在的平面，C是圆周上不同于A，B的任意一点，M，N分别为VA，VC的中点，则下列结论正确的是(　　)

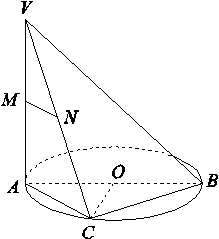
    A．MN∥AB                               B．MN与BC所成的角为45°

    C．OC⊥平面VAC                          D．平面VAC⊥平面VBC


    D

    [解析]　依题意，得BC⊥AC，∵VA⊥平面ABC，BC⊂平面ABC，∴VA⊥BC，∵AC∩VA＝A，∴BC⊥平面VAC，又BC⊂平面VBC，∴平面VAC⊥平面VBC.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    函数单调递增区间是           .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设变量x，y满足约束条件则的最大值是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    从甲、乙等5名志愿者中选出4名，分别从事A，B，C，D四项不同的工作，每人承担一项．若甲、乙二人均不能从事A工作，则不同的工作分配方案共有(　　)

    A．60种  B．72种  C．84种  D．96种

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合M＝{1,2,3,4,5,6}，集合A，B，C为M的非空子集，若∀x∈A，y∈B，z∈C，x<y<z恒成立，则称“A—B—C”为集合M的一个“子集串”，则集合M的“子集串”共有________个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在三棱锥C－ABD中(如图)，△ABD与△CBD是全等的等腰直角三角形，O为斜边BD的中点，AB＝4，二面角A－BD－C的大小为60°，并给出下面结论：①AC⊥BD；②AD⊥CO；③△AOC为正三角形；④cos ∠ADC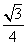＝；⑤四面体ABCD的外接球的表面积为32π.

    其中真命题是(　　)

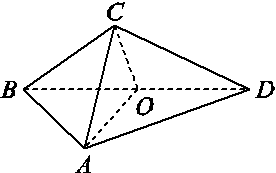
    A．②③④                               B．①③④ 

    C．①④⑤                               D．①③⑤

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    等边三角形ABC的边长为3，点D，E分别是边AB，AC上的点，且满足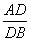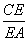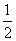＝＝(如图①)．将△ADE沿DE折起到△A1DE的位置，使二面角A1－DE－B为直二面角，连接A1B，A1C(如图②)．

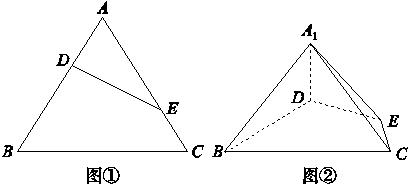
    (1)求证：A1D⊥平面BCED；

    (2)在线段BC上是否存在点P，使直线PA1与平面A1BD所成的角为60°？若存在，求出PB的长，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)为定义在R上的偶函数，当x≥0时，有f(x＋1)＝－f(x)，且当x∈[0,1)时，f(x)＝log2(x＋1)，给出下列命题：

    ①f(2 013)＋f(－2 014)的值为0；

    ②函数f(x)在定义域上为周期是2的周期函数；

    ③直线y＝x与函数f(x)的图象有1个交点；

    ④函数f(x)的值域为(－1,1)．

    其中正确命题的序号有________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设f(x)是定义在R上的偶函数，且当x≥0时，f(x)＝2x.若对任意的x∈[a，a＋2]，不等式f(x＋a)≥f2(x)恒成立，则实数a的取值范围是________．

    查看答案和解析>>

    同步练习册答案