
| A. | -$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ | B. | -$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | C. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | D. | $\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ |
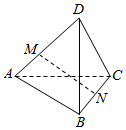
分析 根据题意,利用空间向量的线性表示与运算,用$\overrightarrow{DA}$、$\overrightarrow{DB}$与$\overrightarrow{DC}$表示出$\overrightarrow{MN}$.
解答 解:连接DN,如图所示,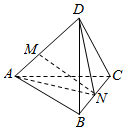
四面体ABCD中,$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DB}$=$\overrightarrow{b}$,$\overrightarrow{DC}$=$\overrightarrow{c}$,
点M在棱DA上,$\overrightarrow{DM}$=2$\overrightarrow{MA}$,∴$\overrightarrow{DM}$=$\frac{2}{3}$$\overrightarrow{DA}$,
又N为BC中点,∴$\overrightarrow{DN}$=$\frac{1}{2}$($\overrightarrow{DB}$+$\overrightarrow{DC}$);
∴$\overrightarrow{MN}$=$\overrightarrow{MD}$+$\overrightarrow{DN}$=-$\frac{2}{3}$$\overrightarrow{DA}$+$\frac{1}{2}$$\overrightarrow{DB}$+$\frac{1}{2}$$\overrightarrow{DC}$=-$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$.
故选:B.
点评 本题考查了空间向量的线性表示与运算问题,是基础题目.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
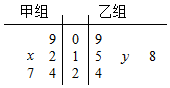 如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为18,乙组数据的中位数为16,则x,y的值分别为( )
如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为18,乙组数据的中位数为16,则x,y的值分别为( )| A. | 18,6 | B. | 8,16 | C. | 8,6 | D. | 18,16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
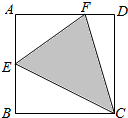 如图,四边形ABCD为正方形,E为AB的中点,F为AD上靠近D的三等分点,若向正方形内随机投掷一个点,则该点落在△CEF内的概率为( )
如图,四边形ABCD为正方形,E为AB的中点,F为AD上靠近D的三等分点,若向正方形内随机投掷一个点,则该点落在△CEF内的概率为( )| A. | $\frac{9}{16}$ | B. | $\frac{7}{16}$ | C. | $\frac{7}{12}$ | D. | $\frac{5}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | $3+2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,7,8} | B. | {4,5,6} | C. | {0,4,5,6} | D. | {0,3,4,5,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p<r<q | B. | q<p<r | C. | r<p<q | D. | p<q<r |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com