
分析 (1)根据递推公式即可求出a2、a3的值;
(2)an+1+3Sn+2=0,①,an+2+3Sn+1+2=0,②,得到an+2=-2an+1,继而得到数列{an}是以-2为首项,以-2为公比的等比数列,问题得以解决;
(3)由题意求出m=(-2)n-4+$\frac{8}{(-2)^{n}+4}$,分别代入n的值求出(m,n)的坐标.
解答 解:(1)a1=-2,an+1+3Sn+2=0(n∈N*),
∴a2+3S1+2=0,a3+3S2+2=0,
∴a2+3a1+2=0,a3+3(a1+a2)+2=0,
∴a2=4,a3=-8,
(2)an+1+3Sn+2=0,①,
an+2+3Sn+1+2=0,②,
②-①得,an+2-an+1+3(Sn+1+Sn)=0,
∴an+2=-2an+1,
∴$\frac{{a}_{n+2}}{{a}_{n+1}}$=-2,
∴数列{an}是以-2为首项,以-2为公比的等比数列,
∴an=-2×(-2)n-1=(-2)n,
(3)∵an2-m•an=4m+8,
∴m=$\frac{{{a}_{n}}^{2}-8}{4+{a}_{n}}$=$\frac{(-2)^{2n}-8}{(-2)^{n}+4}$=$\frac{(-2)^{2n}-16+8}{(-2)^{n}+4}$=(-2)n-4+$\frac{8}{(-2)^{n}+4}$,
∵m为整数,则$\frac{8}{(-2)^{n}+4}$为整数,
当n=1时,m=-2,
当n=2时,m=1,
当n=3时,m=-14,
则满足条件的(m,n)共有(-2,1),(1,2),(-14,3).
点评 本题考查了数列的递推公式,等比数列的通项公式,考查了学生的运算能力,属于中档题.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:选择题
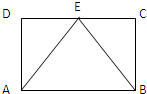 如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机抽取一个点Q,则点Q取自△ABE内部的概率等于( )
如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机抽取一个点Q,则点Q取自△ABE内部的概率等于( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$x-y-4=0 | B. | $\sqrt{3}$x-y-4$\sqrt{3}$=0 | C. | $\sqrt{3}$x+y-4=0 | D. | $\sqrt{3}$x+y-4$\sqrt{3}$=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com