练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．某高中为了解在校高中生对参加某项社会实践活动的意向，拟采用分层抽样的方法从该校三个年级的高中生中抽取一个容量为300的样本进行调查．已知该校高一、高二、高三的人数之比为4：5：6，则应从高一年级抽取80名学生．

    分析 根据分层抽样的定义建立比例关系即可得到结论．

    解答 解：∵高一、高二、高三的人数之比为4：5：6，
    ∴应从高一年级抽取 $\frac{4}{4+5+6}×300$=80，
    故答案为：80

    点评 本题主要考查分层抽样的应用，根据条件建立比例关系是解决本题的关键．比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    4．曲线$\left\{\begin{array}{l}x=2cosθ\\ y=sinθ\end{array}\right.$（θ为参数）上的点到直线$\left\{\begin{array}{l}x=2t\\ y=1+t\end{array}\right.$（t为参数）的距离的最大值为$\frac{2（\sqrt{5}+\sqrt{10}）}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．为了了解城市人均GDP与人均日产生活垃圾量之间的相关关系，国家统计局与卫生管理局随机抽查了6个城市，具体数据如表
    城市天津重庆广州深圳武汉西安
    人均GDP（万美元）x1.640.691.932.221.430.92
    人均日产生活垃圾量（千克）y0.640.511.051.150.990.76
    （1）计算这6个城市人均日产生活垃圾量的平均值（单位：千克）；
    （2）求出x与y之间的线性回归方程；
    （提供下列参考数据：$\sum_{i=1}^6{x_i}=8.82$，$\sum_{i=1}^6{x_i}{y_i}=8.1$，$\sum_{i=1}^6{x_i}^2=14.7$）
    （3）如果某城市的人均GDP达到了3万美元，预测该城市的人均日产生活垃圾量为多少千克？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．不等式x2＞1的解集是（-∞，-1）∪（1，+∞）；不等式-x2+2x+3＞0的解集是（-1，3）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．下面关于算法的说法正确的是（　　）
    A．秦九韶算法是求两个数的最大公约数的方法
    B．更相减损术是求多项式的值的方法
    C．割圆术是采用正多边形面积逐渐逼近圆面积的算法计算圆周率π
    D．以上结论皆错

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．某超市从2014年甲、乙两种酸奶的日销售量（单位：箱）的数据中分别随机抽取100个，整理得到数据分组及频率分布表和频率分布直方图：

    分组
    （日销售量）    		频率
    （甲种酸奶）
    [0，10]0.10
    （10，20]0.20
    （20，30]0.30
    （30，40]0.25
    （40，50]0.15
    （Ⅰ）写出频率分布直方图中的a的值，并作出甲种酸奶日销售量的频率分布直方图；
    答：a=0.015；
    （Ⅱ）记甲种酸奶与乙种酸奶日销售量（单位：箱）的方差分别为s12，s22，试比较s12与s22的大小．（只需写出结论）．
    答：s12＜s22．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知f′（x）是奇函数f（x）的导函数，f（-1）=0，当x＞0时，xf′（x）+f（x）＞0，则使得f（x）＞0成立的x的取值范围是（　　）
    A．（-∞，-1）∪（0，1）B．（-1，0）∪（1，+∞）C．（-1，0）∪（0，1）D．（-∞，-1）∪（1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

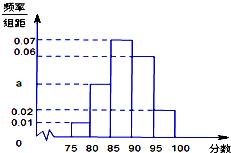    3．某地区有800名学员参加交通法规考试，考试成绩的 频率分 布直
    方图如图所示．其中成绩分组区间是：[75，80﹚，[80，85﹚，
    [85，90﹚，[90，95﹚，[95，100]．规定90分及以上为合格．则（1）图中a的值是0.04；
    （2）根据频率分布直方图估计该地区学员交通法规考试合格的概率是0.4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．${∫}_{0}^{1}$（$\sqrt{1-{x}^{2}}$+x）dx=$\frac{π}{4}$$+\frac{1}{2}$．

    查看答案和解析>>

    同步练习册答案