
| A. | g(x)=$\frac{{x}^{2}}{x}$ | B. | g(x)=($\sqrt{x}$)2 | C. | g(x)=x | D. | g(x)=|x| |
分析 根据两个函数的定义域相同,对应关系也相同,即可判断它们是同一函数.
解答 解:对于A,g(x)=$\frac{{x}^{2}}{x}$=x的定义域是{x|x≠0},f(x)=$\sqrt{{x}^{2}}$=|x|的定义域是R,定义域不同,对应关系也不同,不是同一函数;
对于B,g(x)=${(\sqrt{x})}^{2}$=x的定义域是{x|x≥0},f(x)=$\sqrt{{x}^{2}}$=|x|的定义域是R,定义域不同,对应关系也不同,不是同一函数;
对于C,g(x)=x的定义域是R,f(x)=$\sqrt{{x}^{2}}$=|x|的定义域是R,对应关系不同,不是同一函数;
对于D,g(x)=|x|的定义域是R,f(x)=$\sqrt{{x}^{2}}$=|x|的定义域是R,定义域相同,对应关系也相同,是同一函数.
故选:D.
点评 本题考查了判断两个函数为同一函数的应用问题,是基础题目.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 满意度评分分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | |||||
| 频率 |

| 满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
| 满意度等级 | 不满意 | 满意 | 非常满意 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $20\sqrt{6}$ | B. | 75 | C. | 51 | D. | 49 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
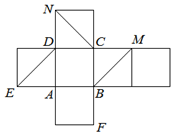 如图是正方体的平面展开图.在这个正方体中,
如图是正方体的平面展开图.在这个正方体中,| A. | ①②③④ | B. | ②④ | C. | ②③④ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com