
���� ������������y=f��x��=k��a-x��x2�����ô���ϵ�����������Ʒ����ֵy����x�ı���ʽ��
���������ĵ��������ݵ����������Ʒ����ֵy�����ֵ����Ӧ��x��ֵ��
��� �⣺��I����y=f��x��=k��a-x��x2��
��Ϊ��x=$\frac{a}{2}$ʱ��y=a3������k=8��
����f��x��=8��a-x��x2��x�ʣ�0��$\frac{4a}{5}$]��
��II����Ϊf�䣨x��=-24x2+16ax����f�䣨x��=0����x=0���ᣩ��x=$\frac{2a}{3}$��
��x�ʣ�0��$\frac{2a}{3}$��ʱ��f�䣨x����0������f��x���ڣ�0��$\frac{2a}{3}$��������������
��x�ʣ�$\frac{2a}{3}$��$\frac{4a}{5}$��ʱ��f�䣨x����0������f��x���ڣ�$\frac{2a}{3}$��$\frac{4a}{5}$�����Ǽ�������
���ԣ���x=$\frac{2a}{3}$ʱ��ymax=f��$\frac{2a}{3}$��=$\frac{32}{27}$a3��
�𣺣�I��f��x��=8��a-x��x2��x�ʣ�0��$\frac{4a}{5}$]����II��Ͷ��$\frac{2a}{3}$��Ԫ���������ֵ$\frac{32}{27}$a3��
�ⷨ������Ϊ$x�ʣ�{0��\frac{4}{5}a}]$������a-x��0��
����$f��x��=8��{a-x}��{x^2}=4��{2a-2x}��•x•x��4��{��{\frac{2a-2x+x+x}{3}}��^3}=\frac{32}{27}{a^3}$
�Ⱥŵ��ҽ���2a-2x=x=x��x=$\frac{2a}{3}$ʱ�Ⱥų�����
��Ϊ$\frac{2a}{3}$�ʣ�0��$\frac{4a}{5}$]�����Ե�x=$\frac{2a}{3}$ʱ��ymax=f��$\frac{2a}{3}$��=$\frac{32}{27}$a3
�𣺣�I��f��x��=8��a-x��x2��x�ʣ�0��$\frac{4a}{5}$]����II��Ͷ��$\frac{2a}{3}$��Ԫ���������ֵ$\frac{32}{27}$a3��
���� ������Ҫ���������е��Ż����⣬���ô���ϵ������������Ľ���ʽ�����õ�����������ֵ�ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
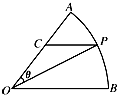 ������AOB�У�Բ�Ľǵ���$\frac{��}{3}$���뾶Ϊ4���ڻ�AB����һ����P�������AB�غϣ�������P��ƽ����OB��ֱ�ߺ�OA���ڵ�C�����AOP=�ȣ���������POC����������ֵ����ʱ�ȵ�ֵ��
������AOB�У�Բ�Ľǵ���$\frac{��}{3}$���뾶Ϊ4���ڻ�AB����һ����P�������AB�غϣ�������P��ƽ����OB��ֱ�ߺ�OA���ڵ�C�����AOP=�ȣ���������POC����������ֵ����ʱ�ȵ�ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9 | B�� | 8 | C�� | 7 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 12 | B�� | 8 | C�� | 6 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{7}$��8n-1�� | B�� | $\frac{2}{7}$��8n+1�� | C�� | $\frac{2}{7}$��8n+1-1�� | D�� | $\frac{2}{7}$��8n+1+1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=tanx | B�� | y=2x | C�� | y=x3 | D�� | y=lg��1+x2�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com