
分析 根据αβ的取值范围,利用同角三角函数的基本关系分别求得cosα和sinβ,由两角差的和正弦公式求得sin(α-β),根据α-β∈($\frac{π}{2}$,$\frac{3π}{2}$),即可求得α-β的值.
解答 解:由α∈($\frac{π}{2}$,π),β∈(-$\frac{π}{2}$,0),sinα=$\frac{\sqrt{5}}{5}$,cosβ=$\frac{\sqrt{10}}{10}$,
∴α-β∈($\frac{π}{2}$,$\frac{3π}{2}$),cosα<0,sinβ<0,
cosα=-$\sqrt{1-si{n}^{2}α}$=-$\sqrt{1-(\frac{\sqrt{5}}{5})^{2}}$=-$\frac{2\sqrt{5}}{5}$,
sinβ=-$\sqrt{1-co{s}^{2}β}$=-$\sqrt{1-(\frac{\sqrt{10}}{10})^{2}}$=-$\frac{3\sqrt{10}}{10}$,
sin(α-β)=sinαcosβ-cosαsinβ,
=$\frac{\sqrt{5}}{5}$×$\frac{\sqrt{10}}{10}$-(-$\frac{2\sqrt{5}}{5}$)(-$\frac{3\sqrt{10}}{10}$),
=-$\frac{\sqrt{2}}{2}$,
∴α-β=$\frac{5π}{4}$.
故答案为:$\frac{5π}{4}$.
点评 本题考查三角函数值的求法,两角和差的正弦公式,同角三角函数的基本关系,属于基础题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 废品率每增加1%,生铁成本增加258元 | |
| B. | 废品率每增加1%,生铁成本增加2元 | |
| C. | 废品率每增加1%,生铁成本每吨增加2元 | |
| D. | 废品率不变,生铁成本为256元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,D、E分别为棱CC1、B1C1的中点,
如图,直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,D、E分别为棱CC1、B1C1的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
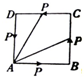 如图,动点P从边长为1的正方形ABCD的顶点A出发,顺次经过B、C、D再回到A.用x表示P点经过的路程,y表示AP的长,则当1<x<2时,$\frac{y^2}{x}$的最小值为( )
如图,动点P从边长为1的正方形ABCD的顶点A出发,顺次经过B、C、D再回到A.用x表示P点经过的路程,y表示AP的长,则当1<x<2时,$\frac{y^2}{x}$的最小值为( )| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 2$\sqrt{2}$-2 | D. | 3$\sqrt{2}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
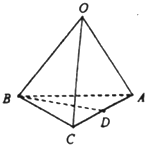 如图,在三棱锥O-ABC中,点D是棱AC的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{BD}$等于( )
如图,在三棱锥O-ABC中,点D是棱AC的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{BD}$等于( )| A. | -$\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$ | B. | $\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com