
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点为
,右焦点为![]() ,左顶点为A,右顶点B在直线
,左顶点为A,右顶点B在直线![]() 上.
上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点P是椭圆C上异于A,B的点,直线![]() 交直线
交直线![]() 于点
于点![]() ,当点
,当点![]() 运动时,判断以
运动时,判断以![]() 为直径的圆与直线PF的位置关系,并加以证明.
为直径的圆与直线PF的位置关系,并加以证明.
【答案】(Ⅰ)![]() ;(Ⅱ)以BD为直径的圆与直线PF相切.
;(Ⅱ)以BD为直径的圆与直线PF相切.
【解析】
(Ⅰ)根据条件解得a,b值,(Ⅱ)设点P(x0,y0),解得D点坐标,即得以BD为直径的圆圆心坐标以及半径,再根据直线PF方程,利用圆心到直线PF距离与半径大小关系作判断.
(Ⅰ)依题可知B(a,0),a=2,因为![]() ,所以c=1,
,所以c=1,![]()
故椭圆C的方程为![]() .
.
(Ⅱ)以BD为直径的圆与直线PF相切.
证明如下:设点P(x0,y0),则![]()
①当x0=1时,点P的坐标为(1,±![]() ),直线PF的方程为x=1,
),直线PF的方程为x=1,
D的坐标为(2,±2).
此时以BD为直径的圆![]() 与直线PF相切.
与直线PF相切.
②当![]() ≠1时直线AP的方程为
≠1时直线AP的方程为![]() ,
,
点D的坐标为![]() ,BD中点E的坐标为
,BD中点E的坐标为![]() ,故
,故![]()
直线PF的斜率为![]() ,
,
故直线PF的方程为![]() ,即
,即![]() ,
,
所以点E到直线PF的距离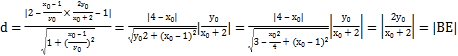 ,故以BD为直径的圆与直线PF相切.
,故以BD为直径的圆与直线PF相切.
综上得,当点P运动时,以BD为直径的圆与直线PF相切.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() .数列
.数列![]() 满足
满足![]() ,
,![]() .
.
(1)若![]() ,且
,且![]() ,求正整数
,求正整数![]() 的值;
的值;
(2)若数列![]() ,
,![]() 均是等差数列,求
均是等差数列,求![]() 的取值范围;
的取值范围;
(3)若数列![]() 是等比数列,公比为
是等比数列,公比为![]() ,且
,且![]() ,是否存在正整数
,是否存在正整数![]() ,使
,使![]() ,
,![]() ,
,![]() 成等差数列,若存在,求出一个
成等差数列,若存在,求出一个![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( ).
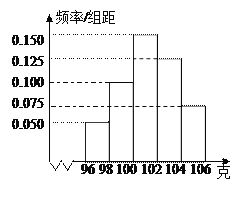
A. 90B. 75C. 60D. 45
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() ,直线
,直线![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,点
,点![]() 和点
和点![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.

(1)若点![]() 是椭圆
是椭圆![]() 的一个焦点,求该椭圆的长轴的长度;
的一个焦点,求该椭圆的长轴的长度;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乳业公司生产甲、乙两种产品,需要A,B,C三种苜蓿草饲料,生产1个单位甲种产品和生产1个单位乙种产品所需三种苜蓿草饲料的吨数如下表所示:
产品 苜蓿草饲料 | A | B | C |
甲 | 4 | 8 | 3 |
乙 | 5 | 5 | 10 |
现有A种饲料200吨,B种饲料360吨,C种饲料300吨,在此基础上生产甲乙两种产品,已知生产1个单位甲产品,产生的利润为2万元;生产1个单位乙产品,产生的利润为3万元,分别用x,y表示生产甲、乙两种产品的数量.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲乙两种产品多少时,能够产出最大的利润?并求出此最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l1:kx-y+4=0与直线l2:x+ky-3=0相交于点P,则当实数k变化时,点P到直线4x-3y+10=0的距离的最大值为( )
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com