Question

18．若函数f（x）=$\left\{\begin{array}{l}{sin（2x-\frac{π}{6}），-π≤x＜m}\\{cos（2x-\frac{π}{6}），m≤x≤\frac{π}{2}}\end{array}\right.$恰有4个零点，则m的取值范围为（　　）

• A． [-$\frac{11π}{12}$，-$\frac{π}{6}$]∪（$\frac{π}{12}$，$\frac{π}{3}$]
• B． （-$\frac{11π}{12}$，-$\frac{2π}{3}$]∪（-$\frac{5π}{12}$，-$\frac{π}{6}$]∪（$\frac{π}{12}$，$\frac{π}{3}$]
• C． [-$\frac{11π}{12}$，-$\frac{π}{6}$）∪[$\frac{π}{12}$，$\frac{π}{3}$）
• D． [-$\frac{11π}{12}$，-$\frac{2π}{3}$）∪[-$\frac{5π}{12}$，-$\frac{π}{6}$）∪[$\frac{π}{12}$，$\frac{π}{3}$）

Answer 1

分析 设g（x）=sin（2x-$\frac{π}{6}$），h（x）=cos（2x-$\frac{π}{6}$），作出这两个函数在[-π，$\frac{π}{2}$]上的图象，求出零点，通过图象即可得到所求m的范围．

解答 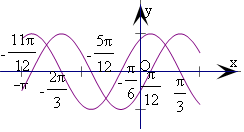解：设g（x）=sin（2x-$\frac{π}{6}$），h（x）=cos（2x-$\frac{π}{6}$），
作出这两个函数在[-π，$\frac{π}{2}$]上的图象，如图所示：
g（x）在[-π，$\frac{π}{2}$]上的零点为-$\frac{11π}{12}$，-$\frac{5π}{12}$，$\frac{π}{12}$；
h（x）在[-π，$\frac{π}{2}$]上的零点为-$\frac{2π}{3}$，-$\frac{π}{6}$，$\frac{π}{3}$．
f（x）恰有4个零点，
由图象可得m∈（-$\frac{11π}{12}$，-$\frac{2π}{3}$]∪（-$\frac{5π}{12}$，-$\frac{π}{6}$]∪（$\frac{π}{12}$，$\frac{π}{3}$]．
故选：B．

点评 本题考查函数的零点个数问题解法，注意运用转化思想和数形结合思想方法，考查观察和判断能力，属于中档题．