
分析 (1)确定|PE|+|PF|=6>2$\sqrt{3}$,可得P的轨迹是以E,F为焦点的椭圆,且a=3,c=$\sqrt{3}$,b=$\sqrt{6}$,即可求C的方程;
(2)将直线方程代入椭圆方程,由韦达定理及中点坐标公式,即可求得M点坐标,由|OM|=1,可得n2=$\frac{(4+{m}^{2})^{2}}{16+{m}^{2}}$,由三角形面积公式,结合换元、配方法即可求得△AOB面积的最大值.
解答 解:(1)设动圆P的半径为r,由已知|PE|=5-r,|PF|=r-1,
则有|PE|+|PF|=4>2$\sqrt{3}$,
∴P的轨迹是以E,F为焦点的椭圆,且a=2,c=$\sqrt{3}$,b=1
∴曲线C的方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1;
(2)设直线l:x=my+n,A(x1,y1),B(x2,y2),
代入椭圆方程,整理得:(4+m2)y2+2mny+n2-4=0①
y1+y2=-$\frac{2mn}{4+{m}^{2}}$,y1•y2=$\frac{{n}^{2}-4}{4+{m}^{2}}$,x1+x2=$\frac{8n}{4+{m}^{2}}$,
由中点坐标公式可知:M($\frac{4n}{4+{m}^{2}}$,-$\frac{mn}{4+{m}^{2}}$)
∵|OM|=1,
∴n2=$\frac{(4+{m}^{2})^{2}}{16+{m}^{2}}$②,…(8分)
设直线l与x轴的交点为D(n,0),
则△AOB面积S2=$\frac{1}{4}$n2(y1-y2)2=$\frac{48({m}^{2}+4)}{(16+{m}^{2})^{2}}$
设t=m2+16(t≥16),
则S2=48($\frac{1}{t}-\frac{12}{{t}^{2}}$),当t=24时,即m=0时,
△AOB的面积取得最大值1…(12分)
点评 本题考查椭圆的标准方程的求法,直线与椭圆的位置关系,韦达定理,及三角形面积公式,考查计算能力,属于中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
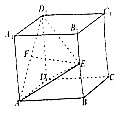 如图,直四棱柱ABCD-A1B1C1D1中,四边形ABCD是菱形,AB=AA1=2,∠ABC=120°,E,F分别为BB1、AD1的中点.
如图,直四棱柱ABCD-A1B1C1D1中,四边形ABCD是菱形,AB=AA1=2,∠ABC=120°,E,F分别为BB1、AD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
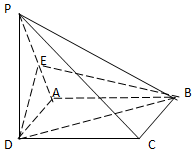 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,求证:
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 空间任三点可以确定一个平面 | |
| B. | 垂直于同一条直线的两条直线必互相平行 | |
| C. | 空间不平行的两条直线必相交 | |
| D. | 既不相交也不平行的两条直线是异面直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com