
| A. | [-$\frac{3}{2}$,0) | B. | [-1,0)∪(0,1] | C. | (0,1] | D. | [1,3] |
分析 利用三角函数的有界性、一次函数的单调性即可得出.
解答 解:f(x)=sin2x+asinx+a-$\frac{3}{a}$,令t=sinx(-1≤t≤1),
则g(t)=t2+at+a-$\frac{3}{a}$,
对任意x∈R,f(x)≤0恒成立的充要条件是$\left\{\begin{array}{l}{g(-1)=1-\frac{3}{a}≤0}\\{g(1)=1+2a-\frac{3}{a}≤0}\end{array}\right.$,
解得a的取值范围是(0,1].
故选:C.
点评 本题考查了通过换元转化为一次函数的单调性、三角函数的有界性等基础知识与基本技能方法,考查了计算能力和转化能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
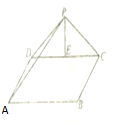 如图所示,在空间四边形ABCD中,AD、CD、AB、BD的中点分别为E、F、G、H.已知AD=1,BC=$\sqrt{3}$,且,对角线$BD=\frac{{\sqrt{13}}}{2},AC=\frac{{\sqrt{3}}}{2}$.求证:△EFG为直角三角形.
如图所示,在空间四边形ABCD中,AD、CD、AB、BD的中点分别为E、F、G、H.已知AD=1,BC=$\sqrt{3}$,且,对角线$BD=\frac{{\sqrt{13}}}{2},AC=\frac{{\sqrt{3}}}{2}$.求证:△EFG为直角三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | 2 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{9}+{y}^{2}$=1 | B. | $\frac{{x}^{2}}{9}+\frac{{y}^{2}}{81}$=1 | ||
| C. | $\frac{{x}^{2}}{9}+{y}^{2}$=1或 $\frac{{x}^{2}}{9}+\frac{{y}^{2}}{81}$=1 | D. | $\frac{{x}^{2}}{81}+\frac{{y}^{2}}{9}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 2 018×2 012 | B. | 2 020×2 013 | C. | 1 009×2 012 | D. | 1 010×2 013 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com