
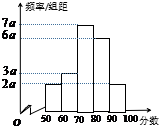
 在一次数学测试中,某班40名学生的成绩频率分布直方图如图所示(学生成绩都在[50,100]之间).
在一次数学测试中,某班40名学生的成绩频率分布直方图如图所示(学生成绩都在[50,100]之间).分析 (Ⅰ)根据频率和为1,列出方程,求出a的值,利用组中值,即可估算该班级的平均分;
(Ⅱ)根据成绩为优秀的有4人,根据互斥事件的概率公式计算即可.
解答 解:(Ⅰ)由题意得,(2a+2a+3a+6a+7a)×10=1,解得a=0.005.
平均成绩约为$55×\frac{2}{20}+65×\frac{3}{20}+75×\frac{7}{20}+85×\frac{6}{20}+95×\frac{2}{20}=76.5$;
(Ⅱ)90分及以上人数为$40×\frac{2}{20}=4$人.
设“至少有一人成绩为优秀”为事件A,则$P(A)=1-\frac{{C_{36}^2}}{{C_{40}^2}}=\frac{5}{26}$
点评 本题考查了频率分布直方图的应用问题,也考查了概率的计算,是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 记忆能力x | 4 | 6 | 8 | 10 |
| 识图能力y | 3 | 5 | 6 | 8 |
| A. | 0.1 | B. | -0.1 | C. | 0.2 | D. | -0.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$ | B. | 0 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 已知a,b,m∈R,命题“若am2<bm2,则a<b”为真命题 | |
| B. | 命题“?x0∈R,x02-x0>0”的否定是“?x∈R,x2-x≤0” | |
| C. | 命题“p且q”为真命题,则命题p和命题q均为真命题 | |
| D. | “x>3”是“x>2”的必要不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com