
| A. | 已知a,b,m∈R,命题“若am2<bm2,则a<b”为真命题 | |
| B. | 命题“?x0∈R,x02-x0>0”的否定是“?x∈R,x2-x≤0” | |
| C. | 命题“p且q”为真命题,则命题p和命题q均为真命题 | |
| D. | “x>3”是“x>2”的必要不充分条件 |
分析 A根据不等式的性质可判断;
B中否命题是先否定条件,再否定结论;
C根据且命题的定义可判断;
D根据充分条件,必要条件的概念判断即可.
解答 解:A中已知a,b,m∈R,由am2<bm2,可知m2>0,可得a<b”,故正确;
B否命题是先否定条件,再否定结论,对存在命题,把存在一个改为任意,再把结论否定,
∴命题“?x0∈R,x02-x0>0”的否定是“?x∈R,x2-x≤0”,故正确;
C命题“p且q”为真命题,可得p真,q真,则命题p和命题q均为真命题,故正确;
D“x>3”可推出“x>2”,反之不一定,故应是充分不必要条件,故错误.
故选:D.
点评 考查了不等式的性质,命题的否命题,存在命题的否命题,属于基础题型,应熟练掌握.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
| 日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
| 温差x(℃) | 10 | 11 | 13 | 12 | 8 |
| 发芽y(颗) | 23 | 25 | 30 | 26 | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
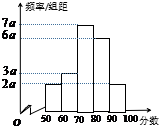 在一次数学测试中,某班40名学生的成绩频率分布直方图如图所示(学生成绩都在[50,100]之间).
在一次数学测试中,某班40名学生的成绩频率分布直方图如图所示(学生成绩都在[50,100]之间).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sin2x)=sinx | B. | f(x2+2x)=|x+1| | C. | f(sin2x)=x2+x | D. | f(x2+1)=|x+1| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com