
分析 (1)求出函数的导数,根据二次函数的性质求出a的范围即可;
(2)①求出f($\frac{{a}^{2}}{4}$)的解析式,求出函数的导数,根据a的范围结合函数的单调性判断即可;②根据f($\frac{1}{x}$)=-f(x),f(1)=0,设出3个零点,从而证出结论.
解答 解:(1)f′(x)=$\frac{{ax}^{2}-2x+a}{{x}^{2}}$,
∵f(x)的定义域是(0,+∞),
∴ax2-2x+a=0有2个不相等的正根,显然a≠0,
由x1x2=1>0,得:$\left\{\begin{array}{l}{△>0}\\{{x}_{1}{+x}_{2}>0}\end{array}\right.$,
解得:0<a<1;
(2)①f($\frac{{a}^{2}}{4}$)=$\frac{{a}^{3}}{4}$-$\frac{4}{a}$-4lna+4ln2,
f′(x)=$\frac{{ax}^{2}-2x+a}{{x}^{2}}$,x∈(0,+∞),
由f(x)有3个极值点,
得ax2-2x+a=0有2个不相等的实数根,
由(1)得:0<a<1,
令h(a)=$\frac{{a}^{3}}{4}$-$\frac{4}{a}$-4lna+4ln2,a∈(0,1),
h′(a)=$\frac{{3a}^{4}+16(1-a)}{{a}^{2}}$,
显然h′(a)>0,故h(a)在(0,1)递增,
故h(a)<h(1)=4ln2-$\frac{15}{4}$<0,
故f($\frac{{a}^{2}}{4}$)<0,
②∵f($\frac{1}{x}$)=a($\frac{1}{x}$-x)-2ln$\frac{1}{x}$=-f(x),
又f(1)=0,得:f(x)的3个零点依次可表达为t,1,$\frac{1}{t}$,t∈(0,1),
故x1+x2+x3=t+1+$\frac{1}{t}$>2+1=3.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式的证明,是一道中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
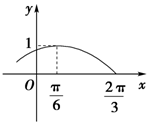 函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$,x∈R)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$,x∈R)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com