
【题目】定义:首项为![]() 且公比为正数的等比数列为“
且公比为正数的等比数列为“![]() 数列”.
数列”.
(Ⅰ)已知等比数列![]() (
(![]() )满足:
)满足:![]() ,
,![]() ,判断数列
,判断数列![]() 是否为“
是否为“![]() 数列”;
数列”;
(Ⅱ)设![]() 为正整数,若存在“
为正整数,若存在“![]() 数列”
数列”![]() (
(![]() ),
),![]() 对任意不大于
对任意不大于![]() 的正整数
的正整数![]() ,都有
,都有![]() 成立,求
成立,求![]() 的最大值.
的最大值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
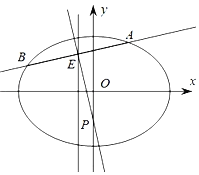
(1)求椭圆C的方程;
(2)直线l交椭圆C于不同的两点A、B,且![]() 中点E在直线
中点E在直线![]() 上,线段
上,线段![]() 的垂直平分线交y轴于点
的垂直平分线交y轴于点![]() ,求m的取值范围.
,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水是生命之源,为了引导市民科学用水,我国加快阶梯水价推行,原则是“保基本、建机制、促节约”,其中“保基本”是指保证至少80%的居民用户用水价格不变,“建机制”是制定合理的阶梯用水价格某城市采用简单随机抽样的方法从郊区和城区分别抽取5户和20户居民的年人均用水量(单位:吨)进行调研,抽取数据的茎叶图如下:
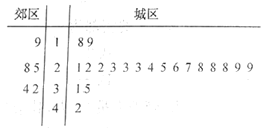
(1)若在郊区的这5户居民中随机抽取2户,求“被抽取的2户年人均用水量的和超过60吨”的概率;
(2)若该城市郊区和城区的居民户数比为1:5,现将年人均用水量不超过30吨的用户定义为第一阶梯用户,只保证这一梯次的居民用户用水价格不变,试根据样本估计总体的思想分析此方案是否符合国家“保基本”政策.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》第![]() 条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”《中华人民共和国道路交通安全法》第
条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”《中华人民共和国道路交通安全法》第![]() 条规定:对不礼让行人的驾驶员处以扣
条规定:对不礼让行人的驾驶员处以扣![]() 分,罚款
分,罚款![]() 元的处罚.下表是某市一主干路口监控设备所抓拍的
元的处罚.下表是某市一主干路口监控设备所抓拍的![]() 个月内驾驶员不“礼让斑马线”行为统计数据:
个月内驾驶员不“礼让斑马线”行为统计数据:
月份 |
|
|
|
|
|
不“礼让斑马线”驾驶员人数 |
|
|
|
|
|
(1)请利用所给数据求不“礼让斑马线”驾驶员人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ,并预测该路口
,并预测该路口![]() 月份的不“礼让斑马线”驾驶员人数;
月份的不“礼让斑马线”驾驶员人数;
(2)若从表中![]() 月份和
月份和![]() 月份的不“礼让斑马线”驾驶员中,采用分层抽样方法抽取一个容量为
月份的不“礼让斑马线”驾驶员中,采用分层抽样方法抽取一个容量为![]() 的样本,再从这
的样本,再从这![]() 人中任选
人中任选![]() 人进行交规调查,求抽到的两人恰好来自同一月份的概率.
人进行交规调查,求抽到的两人恰好来自同一月份的概率.
参考公式: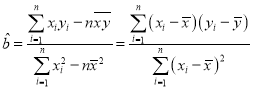 ,
,![]() .
.
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人各进行![]() 次射击,甲每次击中目标的概率为
次射击,甲每次击中目标的概率为![]() ,乙每次击中目标的概率
,乙每次击中目标的概率![]() ,
,
(Ⅰ)记甲击中目标的次数为![]() ,求
,求![]() 的概率分布及数学期望;
的概率分布及数学期望;
(Ⅱ)求甲恰好比乙多击中目标![]() 次的概率.
次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,把边长为4的正![]() 沿中位线
沿中位线![]() 折起使点
折起使点![]() 到
到![]() 的位置.
的位置.
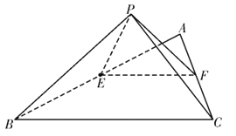
(1)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,确定
?若存在,确定![]() 的位置,若不存在,说明理由;
的位置,若不存在,说明理由;
(2)若![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,
是正方形,![]() 底面
底面![]() ,
,![]() ,点E是
,点E是![]() 的中点,点F在边
的中点,点F在边![]() 上移动.
上移动.
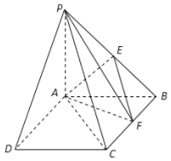
(Ⅰ)若F为![]() 中点,求证:
中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() ;
;
(Ⅲ)若二面角![]() 的余弦值等于
的余弦值等于![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子公司新开发一电子产品,该电子产品的一个系统G有3个电子元件组成,各个电子元件能否正常工作的概率均为![]() ,且每个电子元件能否正常工作相互独立.若系统C中有超过一半的电子元件正常工作,则G可以正常工作,否则就需要维修,且维修所需费用为500元.
,且每个电子元件能否正常工作相互独立.若系统C中有超过一半的电子元件正常工作,则G可以正常工作,否则就需要维修,且维修所需费用为500元.
(1)求系统不需要维修的概率;
(2)该电子产品共由3个系统G组成,设E为电子产品需要维修的系统所需的费用,求![]() 的分布列与期望;
的分布列与期望;
(3)为提高G系统正常工作概率,在系统内增加两个功能完全一样的其他品牌的电子元件,每个新元件正常工作的概率均为![]() ,且新增元件后有超过一半的电子元件正常工作,则C可以正常工作,问:
,且新增元件后有超过一半的电子元件正常工作,则C可以正常工作,问:![]() 满足什么条件时,可以提高整个G系统的正常工作概率?
满足什么条件时,可以提高整个G系统的正常工作概率?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com