
分析 (1)当a=1时,由题可解得A=[0,3],B=[1,3],即可求A∩B;
(2)当集合A,B满足B⊆A时,$\left\{\begin{array}{l}a≥0\\ a+2≤3\end{array}\right.$,即可求实数a取值范围.
解答 解:(1)当a=1时,由题可解得A=[0,3],B=[1,3],…(2分)
A∩B=[1,3]…(4分)
(2)当集合A,B满足B⊆A时,由$\left\{\begin{array}{l}a≥0\\ a+2≤3\end{array}\right.$…(6分)
得实数a的取值范围是[0,1]…(8分)
点评 本题考查集合的关系,考查学生的计算能力,比较基础.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{18}{4a+1}$ | ||
| C. | $\frac{18}{a+4}$或$\frac{18}{4a+1}$ | D. | $\frac{18}{4a+1}$或$\frac{18}{a+4}$或$\frac{9\sqrt{a}}{2a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
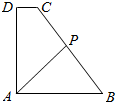 如图,直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=AB=4,CD=1,动点P在边BC上,且满足$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AD}$(m,n均为正实数),则$\frac{1}{m}+\frac{1}{n}$的最小值为$\frac{7+4\sqrt{3}}{4}$.
如图,直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=AB=4,CD=1,动点P在边BC上,且满足$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AD}$(m,n均为正实数),则$\frac{1}{m}+\frac{1}{n}$的最小值为$\frac{7+4\sqrt{3}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | c<b<a | C. | a<b<c | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
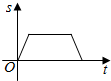 如图是王老师锻炼时所走的离家距离(S)与行走时间(t)之间的函数关系图,若用黑点表示王老师家的位置,则王老师行走的路线可能是( )
如图是王老师锻炼时所走的离家距离(S)与行走时间(t)之间的函数关系图,若用黑点表示王老师家的位置,则王老师行走的路线可能是( )| A. |  | B. | 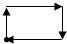 | C. | 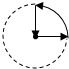 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com