
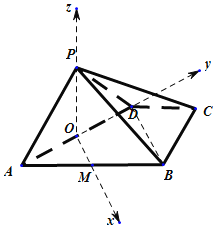
【题目】如图1,在矩形PABC中,AB=2BC=4,D为PC的中点,以AD为折痕将△PAD折起,折到如图2的位置,使得PB=2![]() .
.

(1)求证:AP⊥平面PBD
(2)求平面PCD与平面PBC所成锐二面角的余弦值.
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)通过计算可以发现AP2+BP2=AB2,则AP⊥BP,进而容易得证;
(2)解题的关键是证明平面ABD⊥平面APD,进而可得OP⊥平面ABD,从而建立空间直角坐标系O﹣xyz,由此得解.
(1)由于在矩形PABC中,AB=2BC=4,D为PC的中点,以AD为折痕将△PAD折起,折到如图2的位置,使得PB=2![]() ,所以
,所以![]() ,
,
由于AP2+BP2=AB2,所以AP⊥BP,
又AP⊥PD,BP∩PD=D,且BP,PD都在平面PBD中,
所以AP⊥平面PBD.
(2)取AD的中点O,则AO=OD=OP![]() ,
,![]() ,连接PO,BD,则
,连接PO,BD,则![]() ,
,
∵AB=4,∴AB2=AD2+BD2,即AD⊥BD,
又由(1)知,BD⊥AP,∴BD⊥平面APD,∴平面ABD⊥平面APD,
显然,OP⊥AD,OP⊥平面ABD,
过点O作直线OM∥BD,则OM⊥AD,故建立如图所示空间直角坐标系O﹣xyz,
则![]() ,
,![]() ,
,
设平面PCD的法向量为![]() ,
,
则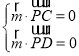 ,即
,即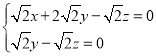 ,令y=z=1,则x=﹣1,故
,令y=z=1,则x=﹣1,故![]() ,
,
设平面PBC的法向量为![]() ,
,
则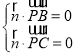 ,即
,即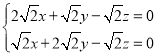 ,令x=y=1,则z=3,故
,令x=y=1,则z=3,故![]() ,
,
∴ ,
,
∴平面PCD与平面PBC所成锐二面角的余弦值为![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:![]() ):男生成绩在175
):男生成绩在175![]() 以上(包括175
以上(包括175![]() )定义为“合格”,成绩在175
)定义为“合格”,成绩在175![]() 以下(不包括175
以下(不包括175![]() )定义为“不合格”.女生成绩在165
)定义为“不合格”.女生成绩在165![]() 以上(包括165
以上(包括165![]() )定义为“合格”,成绩在165
)定义为“合格”,成绩在165![]() 以下(不包括165
以下(不包括165![]() )定义为“不合格”.
)定义为“不合格”.
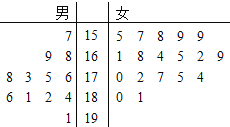
(1)求五年一班的女生立定跳远成绩的中位数;
(2)在五年一班的男生中任意选取3人,求至少有2人的成绩是合格的概率;
(3)若从五年一班成绩“合格”的学生中选取2人参加复试,用![]() 表示其中男生的人数,写出
表示其中男生的人数,写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若![]() =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店计划每天购进某商品若干件,商店每销售一件该商品可获利润60元,若供大于求,剩余商品全部退回,但每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利40元.
(1)若商品一天购进该商品10件,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:件,
(单位:件,![]() )的函数解析式;
)的函数解析式;
(2)商店记录了50天该商品的日需求量![]() (单位:件,
(单位:件,![]() ),整理得下表:
),整理得下表:

若商店一天购进10件该商品,以50天记录的各需求量的频率作为各需求量发生的概率,求当天的利润在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆![]() 上每一点的纵坐标保持不变,横坐标伸长为原来的2倍,得曲线C.
上每一点的纵坐标保持不变,横坐标伸长为原来的2倍,得曲线C.
(Ⅰ)写出曲线C的参数方程;
(Ⅱ)设直线![]() 与曲线C的交点为
与曲线C的交点为![]() 、
、![]() ,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段
,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段![]() 的中点且与
的中点且与![]() 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知![]() ,若线段FP的中垂线l与抛物线C:
,若线段FP的中垂线l与抛物线C:![]() 总是相切.
总是相切.
(1)求抛物线C的方程;
(2)若过点Q(2,1)的直线l′交抛物线C于M,N两点,过M,N分别作抛物线的切线![]() 相交于点A.
相交于点A.![]() 分别与y轴交于点B,C.
分别与y轴交于点B,C.
( i)证明:当![]() 变化时,
变化时,![]() 的外接圆过定点,并求出定点的坐标 ;
的外接圆过定点,并求出定点的坐标 ;
( ii)求![]() 的外接圆面积的最小值.
的外接圆面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点
的左焦点![]() ,离心率为
,离心率为![]() ,点P为椭圆E上任一点,且
,点P为椭圆E上任一点,且![]() 的最大值为
的最大值为![]() .
.
(1)求椭圆E的方程;
(2)若直线l过椭圆的左焦点![]() ,与椭圆交于A,B两点,且
,与椭圆交于A,B两点,且![]() 的面积为
的面积为![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】世界互联网大会是由中国倡导并每年在浙江省嘉兴市桐乡乌镇举办的世界性互联网盛会,大会旨在搭建中国与世界互联互通的国际平台和国际互联网共享共治的中国平台,让各国在争议中求共识在共识中谋合作在合作中创共赢.2019年10月20日至22日,第六届世界互联网大会如期举行,为了大会顺利召开,组委会特招募了1 000名志愿者.某部门为了了解志愿者的基本情况,调查了其中100名志愿者的年龄,得到了他们年龄的中位数为34岁,年龄在![]() 岁内的人数为15,并根据调查结果画出如图所示的频率分布直方图:
岁内的人数为15,并根据调查结果画出如图所示的频率分布直方图:
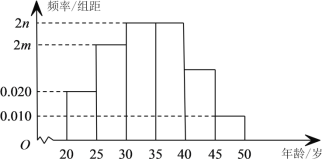
(1)求![]() ,
,![]() 的值并估算出志愿者的平均年龄(同一组的数据用该组区间的中点值代表);
的值并估算出志愿者的平均年龄(同一组的数据用该组区间的中点值代表);
(2)这次大会志愿者主要通过现场报名和登录大会官网报名,即现场和网络两种方式报名调查.这100位志愿者的报名方式部分数据如下表所示,完善下面的表格,通过计算说明能
否在犯错误的概率不超过0.001的前提下,认为“选择哪种报名方式与性别有关系”?
男性 | 女性 | 总计 | |
现场报名 | 50 | ||
网络报名 | 31 | ||
总计 | 50 |
参考公式及数据: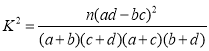 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com